Ross B. McDonald
A probabilistic evolutionary optimization approach to compute quasiparticle braids
Oct 02, 2014


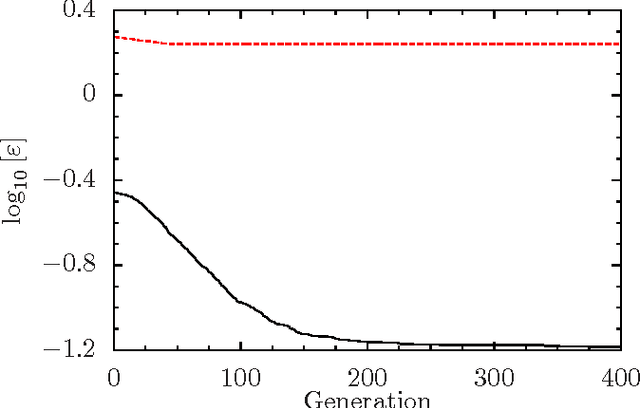
Abstract:Topological quantum computing is an alternative framework for avoiding the quantum decoherence problem in quantum computation. The problem of executing a gate in this framework can be posed as the problem of braiding quasiparticles. Because these are not Abelian, the problem can be reduced to finding an optimal product of braid generators where the optimality is defined in terms of the gate approximation and the braid's length. In this paper we propose the use of different variants of estimation of distribution algorithms to deal with the problem. Furthermore, we investigate how the regularities of the braid optimization problem can be translated into statistical regularities by means of the Boltzmann distribution. We show that our best algorithm is able to produce many solutions that approximates the target gate with an accuracy in the order of $10^{-6}$, and have lengths up to 9 times shorter than those expected from braids of the same accuracy obtained with other methods.
* 9 pages,7 figures. Accepted at SEAL 2014
Genetic braid optimization: A heuristic approach to compute quasiparticle braids
Feb 13, 2013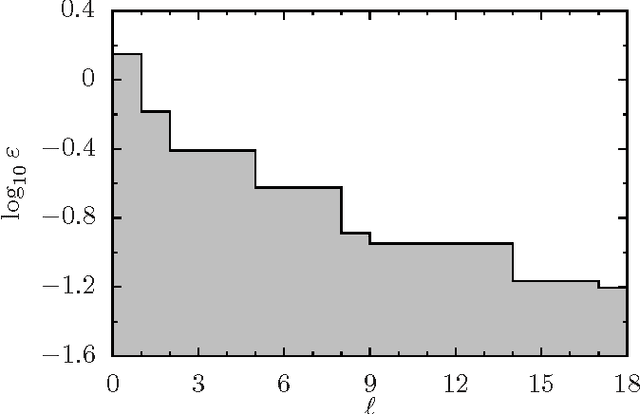

Abstract:In topologically-protected quantum computation, quantum gates can be carried out by adiabatically braiding two-dimensional quasiparticles, reminiscent of entangled world lines. Bonesteel et al. [Phys. Rev. Lett. 95, 140503 (2005)], as well as Leijnse and Flensberg [Phys. Rev. B 86, 104511 (2012)] recently provided schemes for computing quantum gates from quasiparticle braids. Mathematically, the problem of executing a gate becomes that of finding a product of the generators (matrices) in that set that approximates the gate best, up to an error. To date, efficient methods to compute these gates only strive to optimize for accuracy. We explore the possibility of using a generic approach applicable to a variety of braiding problems based on evolutionary (genetic) algorithms. The method efficiently finds optimal braids while allowing the user to optimize for the relative utilities of accuracy and/or length. Furthermore, when optimizing for error only, the method can quickly produce efficient braids.
* 6 pages 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge