Rainbow Deep Q-Learning with Kinematics-Aware Design for Cooperative Delta and 3-RRS Parallel Robot Insertion

This paper presents a kinematics-aware deep reinforcement learning framework based on Rainbow Deep Q-Networks (DQN) for cooperative peg-in-hole manipulation by a Delta parallel robot and a 3-RRS (Revolute--Revolute--Spherical) parallel manipulator. A key contribution is the integration of a geometric design-optimization stage that precedes learning: the 3-RRS geometry is tuned to maximize the singularity-free workspace and improve conditioning, which in turn enlarges the safe region in which the reinforcement learning policy can explore. Together the two manipulators expose a 6~degree-of-freedom (DoF) controllable subspace (three Delta translations, two 3-RRS rotations, and one 3-RRS vertical translation); the peg-in-hole task is invariant to rotation about the peg axis, so the task-relevant manifold is five dimensional. The cooperative insertion problem is cast as a Markov Decision Process with a 12-dimensional state vector and a discrete action set containing $6 \times 2 = 12$ incremental commands (one positive and one negative per controlled DoF). A shaped reward combines dense proximity guidance, penalties for kinematic and workspace violations, and sparse bonuses for successful insertions. The Rainbow DQN -- integrating double Q-learning, dueling architecture, prioritized replay, multi-step returns, noisy linear layers for exploration, and a distributional value head -- is trained with a two-stage curriculum. The co-designed framework is validated in a high-fidelity kinematic simulator, where it achieves stable policy convergence, reliable insertions, and reduced constraint violations compared against a vanilla DQN agent and a classical sampling-based planner.

Quantum Machine Learning and Grover's Algorithm for Quantum Optimization of Robotic Manipulators

Optimizing high-degree of freedom robotic manipulators requires searching complex, high-dimensional configuration spaces, a task that is computationally challenging for classical methods. This paper introduces a quantum native framework that integrates quantum machine learning with Grover's algorithm to solve kinematic optimization problems efficiently. A parameterized quantum circuit is trained to approximate the forward kinematics model, which then constructs an oracle to identify optimal configurations. Grover's algorithm leverages this oracle to provide a quadratic reduction in search complexity. Demonstrated on 1-DoF, 2-DoF, and dual-arm manipulator tasks, the method achieves significant speedups-up to 93x over classical optimizers like Nelder Mead as problem dimensionality increases. This work establishes a foundational, quantum-native framework for robot kinematic optimization, effectively bridging quantum computing and robotics problems.

The Stiffness of 3-PRS PM Across Parasitic and Orientational Workspace

This study investigates the stiffness characteristics of the Sprint Z3 head, also known as 3-PRS Parallel Kinematics Machines, which are among the most extensively researched and viably successful manipulators for precision machining applications. Despite the wealth of research on these robotic manipulators, no previous work has demonstrated their stiffness performance within the parasitic motion space. Such an undesired motion influences their stiffness properties, as stiffness is configuration-dependent. Addressing this gap, this paper develops a stiffness model that accounts for both the velocity-level parasitic motion space and the regular workspace. Numerical simulations are provided to illustrate the stiffness characteristics of the manipulator across all considered spaces. The results indicate that the stiffness profile within the parasitic motion space is both shallower and the values are smaller when compared to the stiffness distribution across the orientation workspace. This implies that evaluating a manipulator's performance adequately requires assessing its ability to resist external loads during parasitic motion. Therefore, comprehending this aspect is crucial for redesigning components to enhance overall stiffness.

Comparing Z3 and A3 PKM Heads: Which Is Superior and Why?

This study presents a comparison between the Sprint Z3 and A3 head parallel kinematics machines, distinguished by their joint sequence. The analysis focuses on performance attributes critical for precision machining specifically, parasitic motion, workspace capability, stiffness performance over the independent and parasitic spaces, and condition number distribution. Although these machines are extensively utilized in precision machining for the aerospace and automotive industries, a definitive superior choice has not been identified for machining large components. Moreover, the distribution of stiffness across the configuration of parasitic space has not previously been addressed for either mechanism. This research reveals that despite identical parameters used and exhibiting similar parasitic motions, the Sprint Z3 demonstrates superior stiffness, workspace volume, and condition number distribution. This performance advantage is attributed to variations in joint and link sequence, which enhance deflection resilience, crucial for manufacturing large-scale components. This also results in a higher condition number and a larger workspace. The result highlights the importance of design architecture in the efficacy of parallel kinematics machines and suggest

Under-actuated Robotic Gripper with Multiple Grasping Modes Inspired by Human Finger

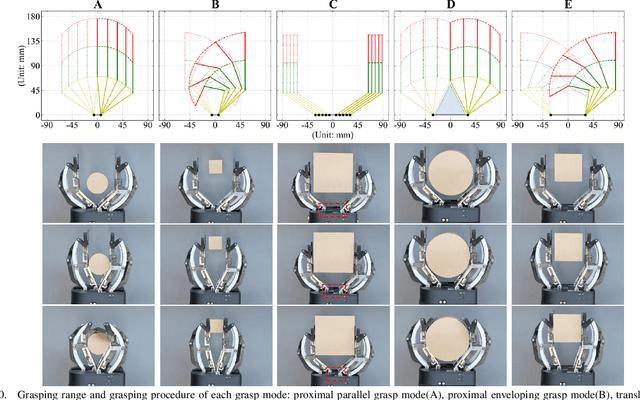
Under-actuated robot grippers as a pervasive tool of robots have become a considerable research focus. Despite their simplicity of mechanical design and control strategy, they suffer from poor versatility and weak adaptability, making widespread applications limited. To better relieve relevant research gaps, we present a novel 3-finger linkage-based gripper that realizes retractable and reconfigurable multi-mode grasps driven by a single motor. Firstly, inspired by the changes that occurred in the contact surface with a human finger moving, we artfully design a slider-slide rail mechanism as the phalanx to achieve retraction of each finger, allowing for better performance in the enveloping grasping mode. Secondly, a reconfigurable structure is constructed to broaden the grasping range of objects' dimensions for the proposed gripper. By adjusting the configuration and gesture of each finger, the gripper can achieve five grasping modes. Thirdly, the proposed gripper is just actuated by a single motor, yet it can be capable of grasping and reconfiguring simultaneously. Finally, various experiments on grasps of slender, thin, and large-volume objects are implemented to evaluate the performance of the proposed gripper in practical scenarios, which demonstrates the excellent grasping capabilities of the gripper.

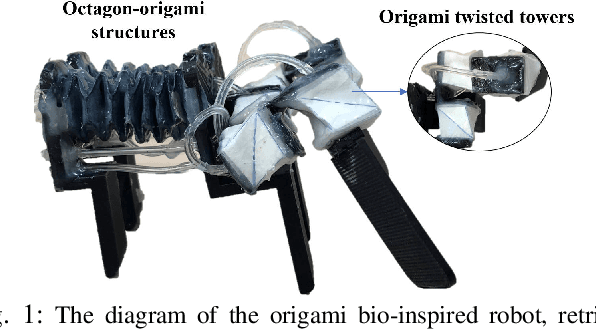
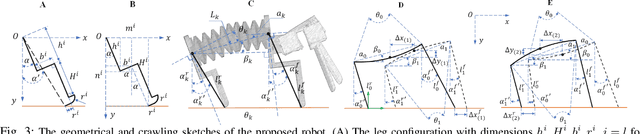
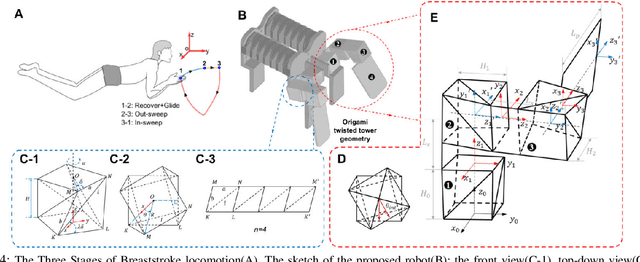
Theoretical Modeling and Bio-inspired Trajectory Optimization of A Multiple-locomotion Origami Robot

Recent research on mobile robots has focused on increasing their adaptability to unpredictable and unstructured environments using soft materials and structures. However, the determination of key design parameters and control over these compliant robots are predominantly iterated through experiments, lacking a solid theoretical foundation. To improve their efficiency, this paper aims to provide mathematics modeling over two locomotion, crawling and swimming. Specifically, a dynamic model is first devised to reveal the influence of the contact surfaces' frictional coefficients on displacements in different motion phases. Besides, a swimming kinematics model is provided using coordinate transformation, based on which, we further develop an algorithm that systematically plans human-like swimming gaits, with maximum thrust obtained. The proposed algorithm is highly generalizable and has the potential to be applied in other soft robots with multiple joints. Simulation experiments have been conducted to illustrate the effectiveness of the proposed modeling.

Unveiling the Complete Variant of Spherical Robots

This study presents a systematic enumeration of spherical ($SO(3)$) type parallel robots' variants using an analytical velocity-level approach. These robots are known for their ability to perform arbitrary rotations around a fixed point, making them suitable for numerous applications. Despite their architectural diversity, existing research has predominantly approached them on a case-by-case basis. This approach hinders the exploration of all possible variants, thereby limiting the benefits derived from architectural diversity. By employing a generalized analytical approach through the reciprocal screw method, we systematically explore all the kinematic conditions for limbs yielding $SO(3)$ motion.Consequently, all 73 possible types of non-redundant limbs suitable for generating the target $SO(3)$ motion are identified. The approach involves performing an in-depth algebraic motion-constraint analysis and identifying common characteristics among different variants. This leads us to systematically explore all 73 symmetric and 5256 asymmetric variants, which in turn become a total of 5329, each potentially having different workspace capability, stiffness performance, and dynamics. Hence, having all these variants can facilitate the innovation of novel spherical robots and help us easily find the best and optimal ones for our specific applications.

Workspace optimization of 1T2R parallel manipulators with a dimensionally homogeneous constraint-embedded Jacobian

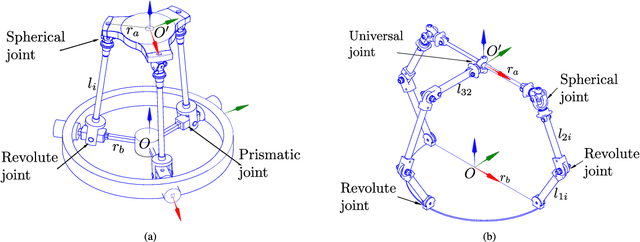
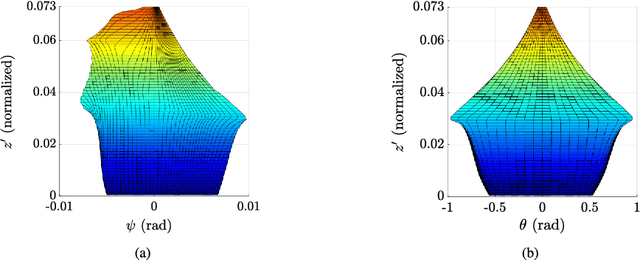
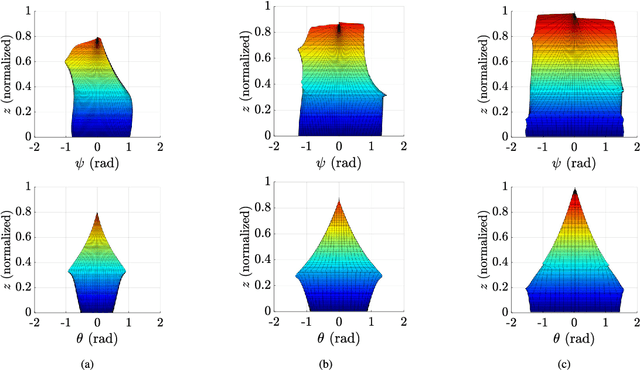
This paper presents the workspace optimization of one-translational two-rotational (1T2R) parallel manipulators using a dimensionally homogeneous constraint-embedded Jacobian. The mixed degrees of freedom of 1T2R parallel manipulators, which cause dimensional inconsistency, make it difficult to optimize their architectural parameters. To solve this problem, a point-based approach with a shifting property, selection matrix, and constraint-embedded inverse Jacobian is proposed. A simplified formulation is provided, eliminating the complex partial differentiation required in previous approaches. The dimensional homogeneity of the proposed method was analytically proven, and its validity was confirmed by comparing it with the conventional point-based method using a 3-PRS manipulator. Furthermore, the approach was applied to an asymmetric 2-RRS/RRRU manipulator with no parasitic motion. This mechanism has a T-shape combination of limbs with different kinematic parameters, making it challenging to derive a dimensionally homogeneous Jacobian using the conventional method. Finally, optimization was performed, and the results show that the proposed method is more efficient than the conventional approach. The efficiency and simplicity of the proposed method were verified using two distinct parallel manipulators.

Dimensionally Homogeneous Jacobian using Extended Selection Matrix for Performance Evaluation and Optimization of Parallel Manipulators

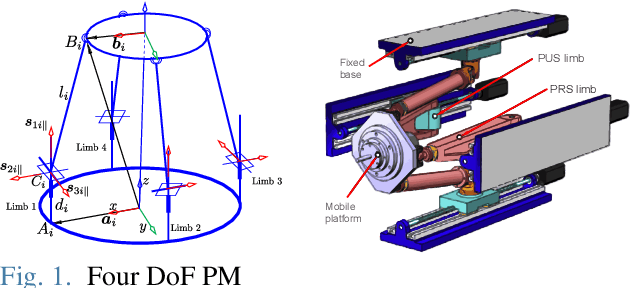
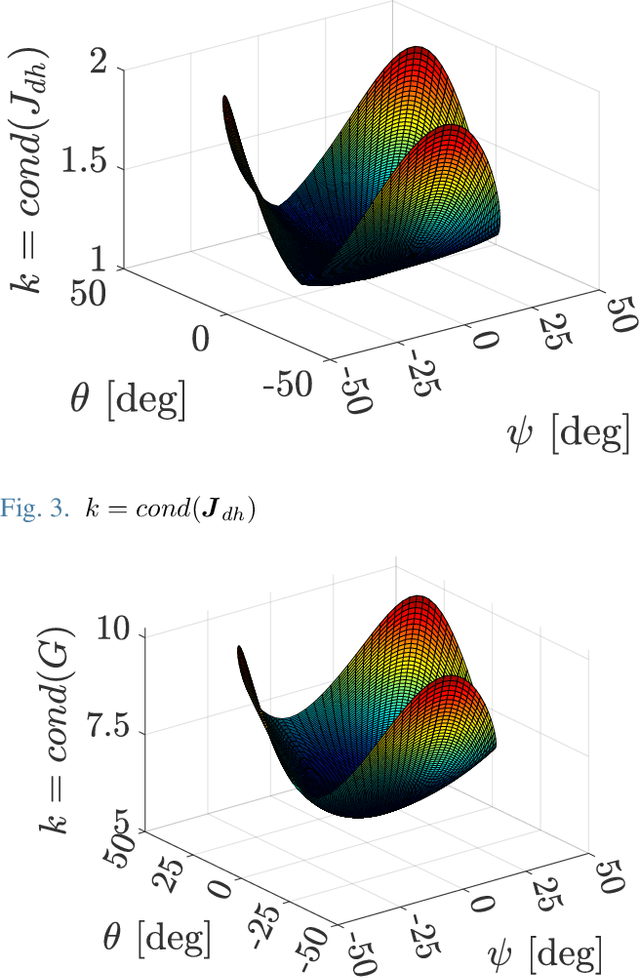
This paper proposes a new methodology for deriving a point-based dimensionally homogeneous Jacobian, intended for performance evaluation and optimization of parallel manipulators with mixed degrees of freedom. Optimal manipulator often rely on performance indices obtained from the Jacobian matrix. However, when manipulators exhibit mixed translational and rotational freedoms, the conventional Jacobian's inconsistency of units lead to unbalanced optimal result. Addressing this issue, a point-based dimensionally homogeneous Jacobian has appeared as a prominent solution. However, existing point-based approaches for formulating dimensionally homogeneous Jacobian are applicable to a limited variety of parallel manipulators. Moreover, they are complicated and less intuitive. This paper introduces an extended selection matrix that combines component velocities from different points to describe the entire motion of moving plate. This proposed approach enables us to formulate an intuitive point-based, dimensionally homogeneous Jacobian, which can be applied to a wide variety of constrained parallel manipulators. To prove the validity of proposed method, a numerical example is provided utilizing a four-degree-of-freedom parallel manipulator.