Workspace optimization of 1T2R parallel manipulators with a dimensionally homogeneous constraint-embedded Jacobian
Paper and Code
Nov 02, 2023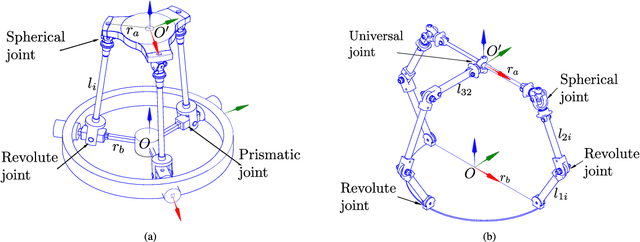

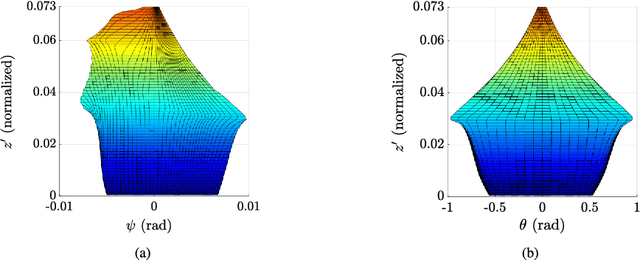
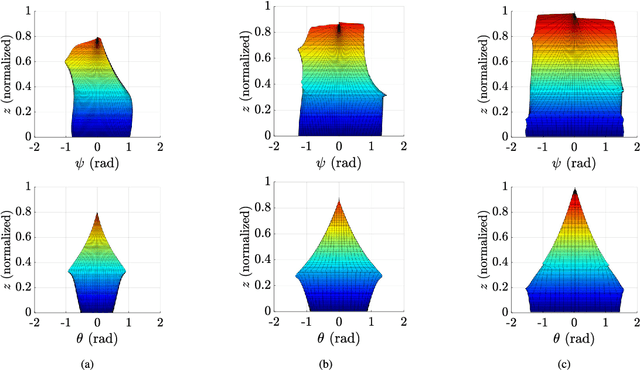
This paper presents the workspace optimization of one-translational two-rotational (1T2R) parallel manipulators using a dimensionally homogeneous constraint-embedded Jacobian. The mixed degrees of freedom of 1T2R parallel manipulators, which cause dimensional inconsistency, make it difficult to optimize their architectural parameters. To solve this problem, a point-based approach with a shifting property, selection matrix, and constraint-embedded inverse Jacobian is proposed. A simplified formulation is provided, eliminating the complex partial differentiation required in previous approaches. The dimensional homogeneity of the proposed method was analytically proven, and its validity was confirmed by comparing it with the conventional point-based method using a 3-PRS manipulator. Furthermore, the approach was applied to an asymmetric 2-RRS/RRRU manipulator with no parasitic motion. This mechanism has a T-shape combination of limbs with different kinematic parameters, making it challenging to derive a dimensionally homogeneous Jacobian using the conventional method. Finally, optimization was performed, and the results show that the proposed method is more efficient than the conventional approach. The efficiency and simplicity of the proposed method were verified using two distinct parallel manipulators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge