The Stiffness of 3-PRS PM Across Parasitic and Orientational Workspace

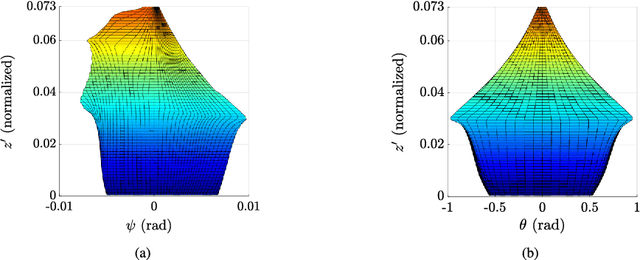
This study investigates the stiffness characteristics of the Sprint Z3 head, also known as 3-PRS Parallel Kinematics Machines, which are among the most extensively researched and viably successful manipulators for precision machining applications. Despite the wealth of research on these robotic manipulators, no previous work has demonstrated their stiffness performance within the parasitic motion space. Such an undesired motion influences their stiffness properties, as stiffness is configuration-dependent. Addressing this gap, this paper develops a stiffness model that accounts for both the velocity-level parasitic motion space and the regular workspace. Numerical simulations are provided to illustrate the stiffness characteristics of the manipulator across all considered spaces. The results indicate that the stiffness profile within the parasitic motion space is both shallower and the values are smaller when compared to the stiffness distribution across the orientation workspace. This implies that evaluating a manipulator's performance adequately requires assessing its ability to resist external loads during parasitic motion. Therefore, comprehending this aspect is crucial for redesigning components to enhance overall stiffness.

Workspace optimization of 1T2R parallel manipulators with a dimensionally homogeneous constraint-embedded Jacobian

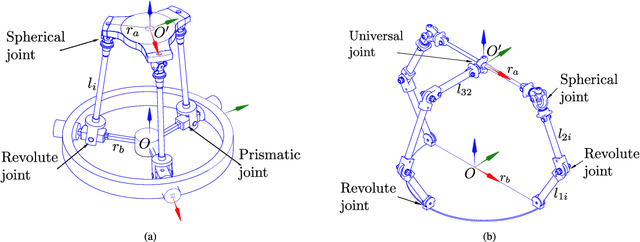
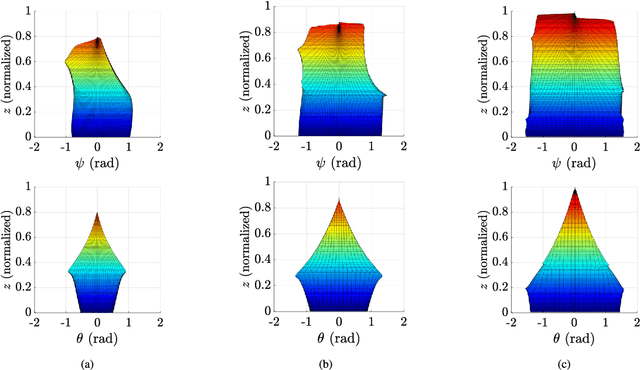
This paper presents the workspace optimization of one-translational two-rotational (1T2R) parallel manipulators using a dimensionally homogeneous constraint-embedded Jacobian. The mixed degrees of freedom of 1T2R parallel manipulators, which cause dimensional inconsistency, make it difficult to optimize their architectural parameters. To solve this problem, a point-based approach with a shifting property, selection matrix, and constraint-embedded inverse Jacobian is proposed. A simplified formulation is provided, eliminating the complex partial differentiation required in previous approaches. The dimensional homogeneity of the proposed method was analytically proven, and its validity was confirmed by comparing it with the conventional point-based method using a 3-PRS manipulator. Furthermore, the approach was applied to an asymmetric 2-RRS/RRRU manipulator with no parasitic motion. This mechanism has a T-shape combination of limbs with different kinematic parameters, making it challenging to derive a dimensionally homogeneous Jacobian using the conventional method. Finally, optimization was performed, and the results show that the proposed method is more efficient than the conventional approach. The efficiency and simplicity of the proposed method were verified using two distinct parallel manipulators.

Dimensionally Homogeneous Jacobian using Extended Selection Matrix for Performance Evaluation and Optimization of Parallel Manipulators

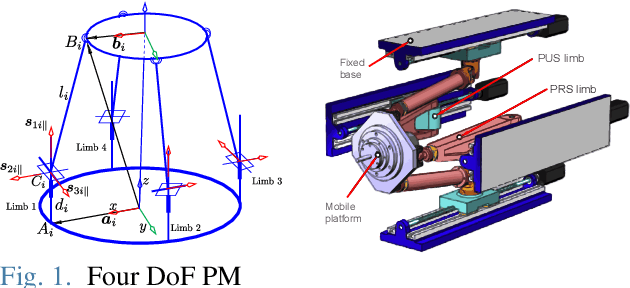
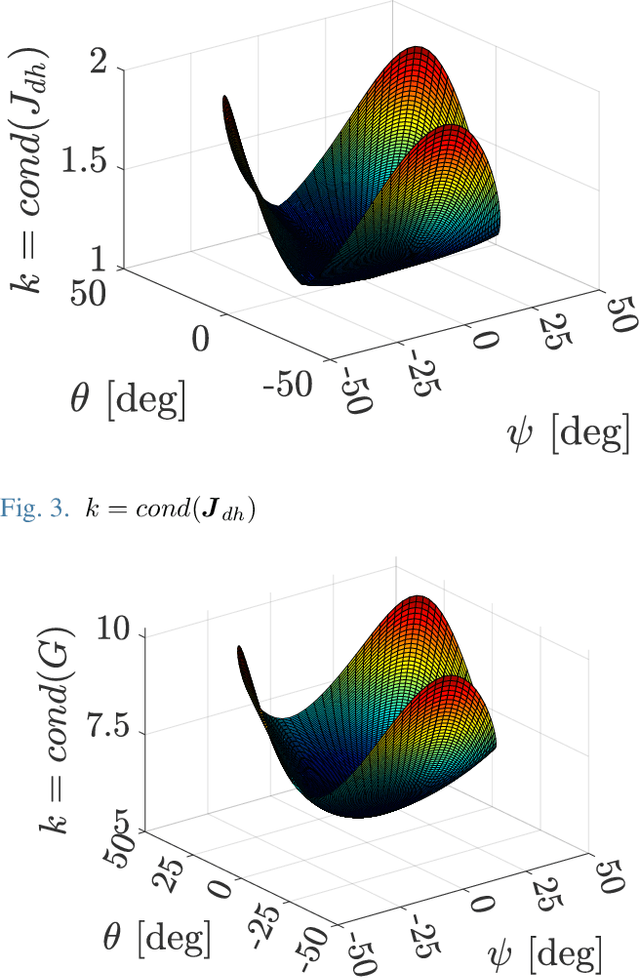
This paper proposes a new methodology for deriving a point-based dimensionally homogeneous Jacobian, intended for performance evaluation and optimization of parallel manipulators with mixed degrees of freedom. Optimal manipulator often rely on performance indices obtained from the Jacobian matrix. However, when manipulators exhibit mixed translational and rotational freedoms, the conventional Jacobian's inconsistency of units lead to unbalanced optimal result. Addressing this issue, a point-based dimensionally homogeneous Jacobian has appeared as a prominent solution. However, existing point-based approaches for formulating dimensionally homogeneous Jacobian are applicable to a limited variety of parallel manipulators. Moreover, they are complicated and less intuitive. This paper introduces an extended selection matrix that combines component velocities from different points to describe the entire motion of moving plate. This proposed approach enables us to formulate an intuitive point-based, dimensionally homogeneous Jacobian, which can be applied to a wide variety of constrained parallel manipulators. To prove the validity of proposed method, a numerical example is provided utilizing a four-degree-of-freedom parallel manipulator.