On the Interaction of Adaptive Population Control with Cumulative Step-Size Adaptation

Three state-of-the-art adaptive population control strategies (PCS) are theoretically and empirically investigated for a multi-recombinative, cumulative step-size adaptation Evolution Strategy $(\mu/\mu_I, \lambda)$-CSA-ES. First, scaling properties for the generation number and mutation strength rescaling are derived on the sphere in the limit of large population sizes. Then, the adaptation properties of three standard CSA-variants are studied as a function of the population size and dimensionality, and compared to the predicted scaling results. Thereafter, three PCS are implemented along the CSA-ES and studied on a test bed of sphere, random, and Rastrigin functions. The CSA-adaptation properties significantly influence the performance of the PCS, which is shown in more detail. Given the test bed, well-performing parameter sets (in terms of scaling, efficiency, and success rate) for both the CSA- and PCS-subroutines are identified.

Mutation Strength Adaptation of the $(μ/μ_I, λ)$-ES for Large Population Sizes on the Sphere Function

The mutation strength adaptation properties of a multi-recombinative $(\mu/\mu_I, \lambda)$-ES are studied for isotropic mutations. To this end, standard implementations of cumulative step-size adaptation (CSA) and mutative self-adaptation ($\sigma$SA) are investigated experimentally and theoretically by assuming large population sizes ($\mu$) in relation to the search space dimensionality ($N$). The adaptation is characterized in terms of the scale-invariant mutation strength on the sphere in relation to its maximum achievable value for positive progress. %The results show how the different $\sigma$-adaptation variants behave as $\mu$ and $N$ are varied. Standard CSA-variants show notably different adaptation properties and progress rates on the sphere, becoming slower or faster as $\mu$ or $N$ are varied. This is shown by investigating common choices for the cumulation and damping parameters. Standard $\sigma$SA-variants (with default learning parameter settings) can achieve faster adaptation and larger progress rates compared to the CSA. However, it is shown how self-adaptation affects the progress rate levels negatively. Furthermore, differences regarding the adaptation and stability of $\sigma$SA with log-normal and normal mutation sampling are elaborated.

Analyzing design principles for competitive evolution strategies in constrained search spaces

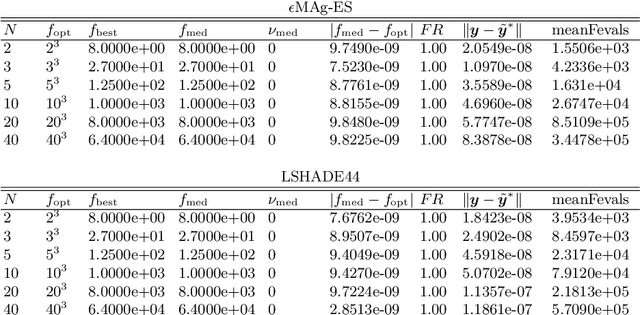
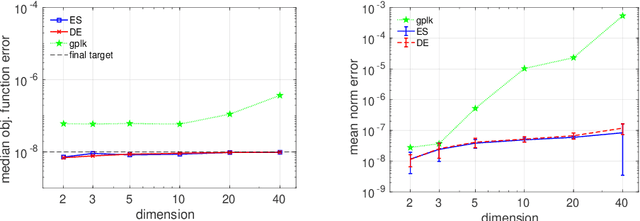
In the context of the 2018 IEEE Congress of Evolutionary Computation, the Matrix Adaptation Evolution Strategy for constrained optimization turned out to be notably successful in the competition on constrained single objective real-parameter optimization. Across all considered instances the so-called $\epsilon$MAg-ES achieved the second rank. However, it can be considered to be the most successful participant in high dimensions. Unfortunately, the competition result does not provide any information about the modus operandi of a successful algorithm or its suitability for problems of a particular shape. To this end, the present paper is concerned with an extensive empirical analysis of the $\epsilon$MAg-ES working principles that is expected to provide insights about the performance contribution of specific algorithmic components. To avoid rankings with respect to insignificant differences within the algorithm realizations, the paper additionally introduces significance testing into the ranking process.

Analysis of the $$-CSA-ES with Repair by Projection Applied to a Conically Constrained Problem

Theoretical analyses of evolution strategies are indispensable for gaining a deep understanding of their inner workings. For constrained problems, rather simple problems are of interest in the current research. This work presents a theoretical analysis of a multi-recombinative evolution strategy with cumulative step size adaptation applied to a conically constrained linear optimization problem. The state of the strategy is modeled by random variables and a stochastic iterative mapping is introduced. For the analytical treatment, fluctuations are neglected and the mean value iterative system is considered. Non-linear difference equations are derived based on one-generation progress rates. Based on that, expressions for the steady state of the mean value iterative system are derived. By comparison with real algorithm runs, it is shown that for the considered assumptions, the theoretical derivations are able to predict the dynamics and the steady state values of the real runs.

Analysis of the $(μ/μ_I,λ)$-$σ$-Self-Adaptation Evolution Strategy with Repair by Projection Applied to a Conically Constrained Problem

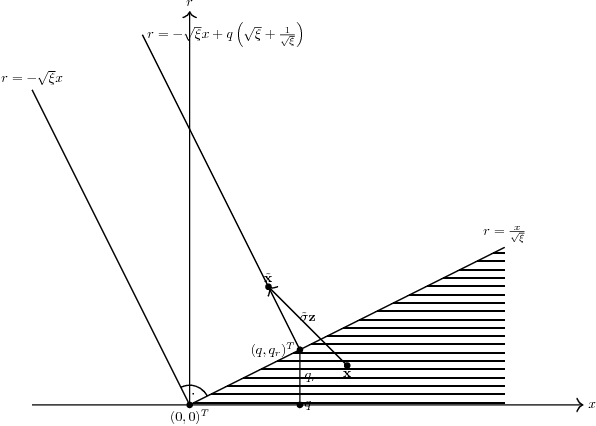
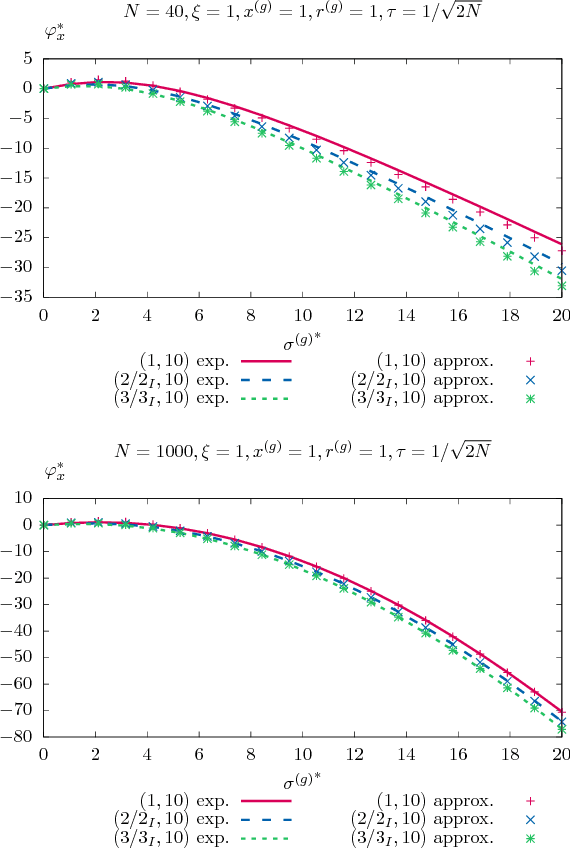
A theoretical performance analysis of the $(\mu/\mu_I,\lambda)$-$\sigma$-Self-Adaptation Evolution Strategy ($\sigma$SA-ES) is presented considering a conically constrained problem. Infeasible offspring are repaired using projection onto the boundary of the feasibility region. Closed-form approximations are used for the one-generation progress of the evolution strategy. Approximate deterministic evolution equations are formulated for analyzing the strategy's dynamics. By iterating the evolution equations with the approximate one-generation expressions, the evolution strategy's dynamics can be predicted. The derived theoretical results are compared to experiments for assessing the approximation quality. It is shown that in the steady state the $(\mu/\mu_I,\lambda)$-$\sigma$SA-ES exhibits a performance as if the ES were optimizing a sphere model. Unlike the non-recombinative $(1,\lambda)$-ES, the parental steady state behavior does not evolve on the cone boundary but stays away from the boundary to a certain extent.

Benchmarking Evolutionary Algorithms For Single Objective Real-valued Constrained Optimization - A Critical Review

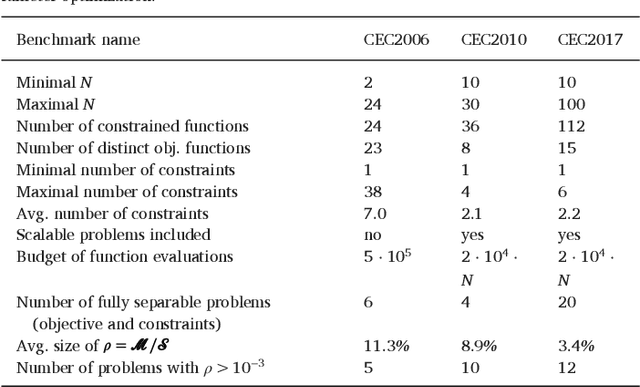
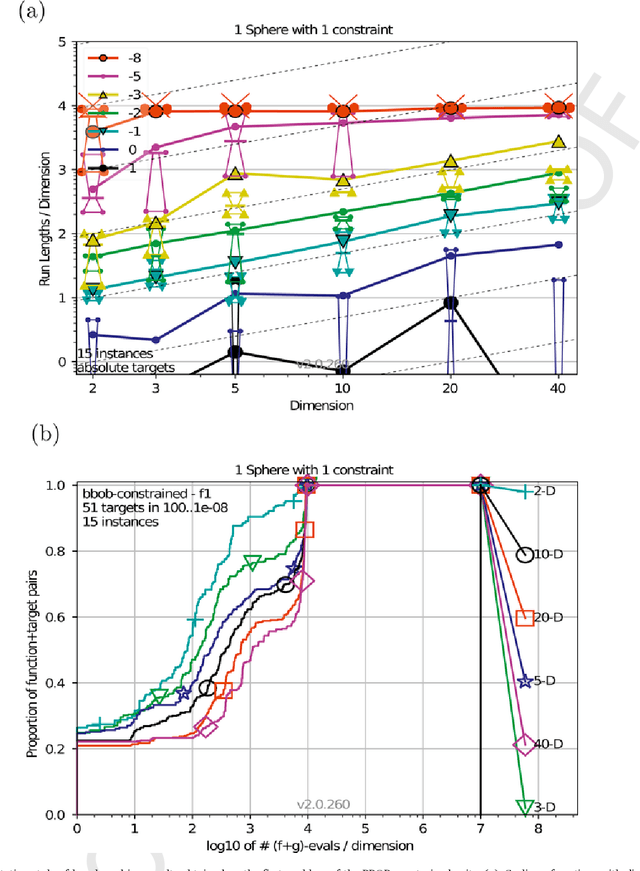
Benchmarking plays an important role in the development of novel search algorithms as well as for the assessment and comparison of contemporary algorithmic ideas. This paper presents common principles that need to be taken into account when considering benchmarking problems for constrained optimization. Current benchmark environments for testing Evolutionary Algorithms are reviewed in the light of these principles. Along with this line, the reader is provided with an overview of the available problem domains in the field of constrained benchmarking. Hence, the review supports algorithms developers with information about the merits and demerits of the available frameworks.

A Covariance Matrix Self-Adaptation Evolution Strategy for Optimization under Linear Constraints

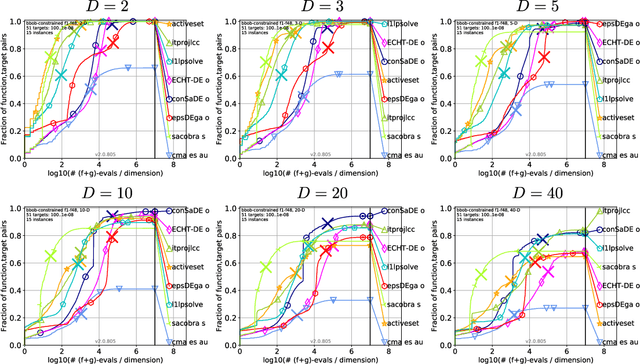
This paper addresses the development of a covariance matrix self-adaptation evolution strategy (CMSA-ES) for solving optimization problems with linear constraints. The proposed algorithm is referred to as Linear Constraint CMSA-ES (lcCMSA-ES). It uses a specially built mutation operator together with repair by projection to satisfy the constraints. The lcCMSA-ES evolves itself on a linear manifold defined by the constraints. The objective function is only evaluated at feasible search points (interior point method). This is a property often required in application domains such as simulation optimization and finite element methods. The algorithm is tested on a variety of different test problems revealing considerable results.

A Linear Constrained Optimization Benchmark For Probabilistic Search Algorithms: The Rotated Klee-Minty Problem

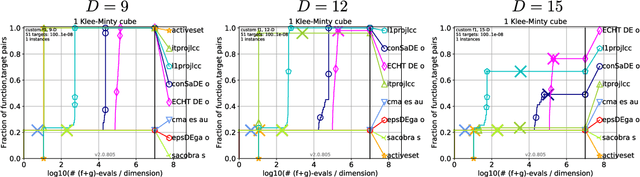
The development, assessment, and comparison of randomized search algorithms heavily rely on benchmarking. Regarding the domain of constrained optimization, the number of currently available benchmark environments bears no relation to the number of distinct problem features. The present paper advances a proposal of a scalable linear constrained optimization problem that is suitable for benchmarking Evolutionary Algorithms. By comparing two recent EA variants, the linear benchmarking environment is demonstrated.

Limited-Memory Matrix Adaptation for Large Scale Black-box Optimization

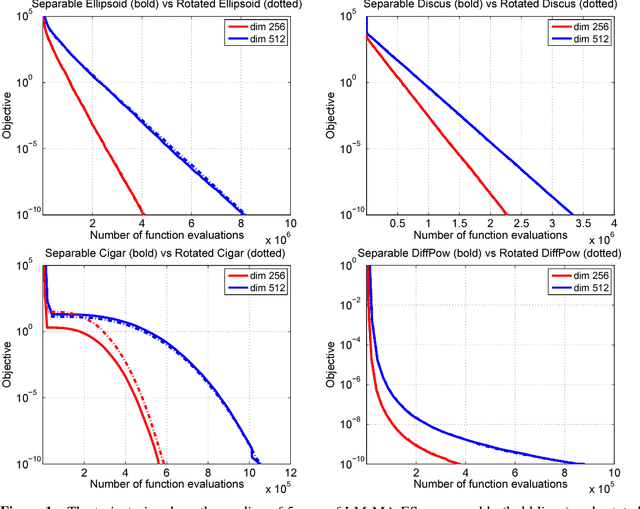
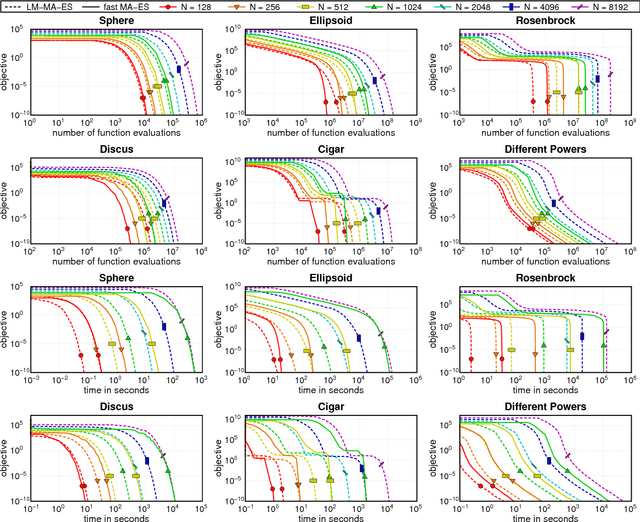
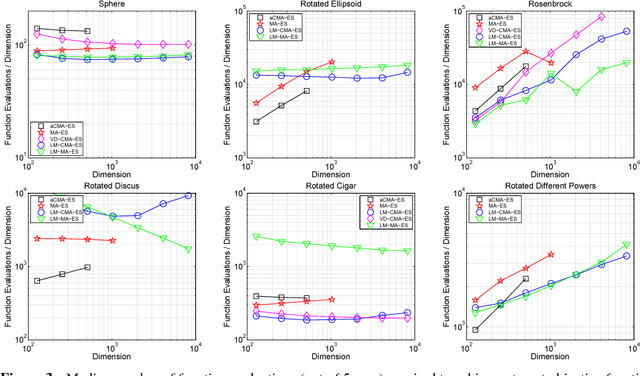
The Covariance Matrix Adaptation Evolution Strategy (CMA-ES) is a popular method to deal with nonconvex and/or stochastic optimization problems when the gradient information is not available. Being based on the CMA-ES, the recently proposed Matrix Adaptation Evolution Strategy (MA-ES) provides a rather surprising result that the covariance matrix and all associated operations (e.g., potentially unstable eigendecomposition) can be replaced in the CMA-ES by a updated transformation matrix without any loss of performance. In order to further simplify MA-ES and reduce its $\mathcal{O}\big(n^2\big)$ time and storage complexity to $\mathcal{O}\big(n\log(n)\big)$, we present the Limited-Memory Matrix Adaptation Evolution Strategy (LM-MA-ES) for efficient zeroth order large-scale optimization. The algorithm demonstrates state-of-the-art performance on a set of established large-scale benchmarks. We explore the algorithm on the problem of generating adversarial inputs for a (non-smooth) random forest classifier, demonstrating a surprising vulnerability of the classifier.