Comprehensive Benchmarking Environment for Worker Flexibility in Flexible Job Shop Scheduling Problems

In Production Scheduling, the Flexible Job Shop Scheduling Problem (FJSSP) aims to optimize a sequence of operations and assign each to an eligible machine with varying processing times. For integration of the workforce, each machine also requires a worker to be present to process an operation which additionally affects the processing times. The resulting problem is called Flexible Job Shop Scheduling Problem with Worker Flexibility (FJSSP-W). The FJSSP has been approached with various problem representations, including Mixed Integer Linear Programming (MILP), Constrained Programming (CP), and Simulation-based Optimization (SBO). In the latter area in particular, there exists a large number of specialized Evolutionary Algorithms (EA) like Particle Swarm Optimization (PSO) or Genetic Algorithms (GA). Yet, the solvers are often developed for single use cases only, and validated on a few selected test instances, let alone compared with results from solvers using other problem representations. While suitable approaches do also exist, the design of the FJSSP-W instances is not standardized and the algorithms are hardly comparable. This calls for a systematic benchmarking environment that provides a comprehensive set of FJSSP(-W) instances and supports targeted algorithm development. It will facilitate the comparison of algorithmic performance in the face of different problem characteristics. The present paper presents a collection of 402 commonly accepted FJSSP instances and proposes an approach to extend these with worker flexibility. In addition, we present a detailed procedure for the evaluation of scheduling algorithms on these problem sets and provide suitable model representations for this purpose. We provide complexity characteristics for all presented instances as well as baseline results of common commercial solvers to facilitate the validation of new algorithmic developments.

Analyzing design principles for competitive evolution strategies in constrained search spaces

In the context of the 2018 IEEE Congress of Evolutionary Computation, the Matrix Adaptation Evolution Strategy for constrained optimization turned out to be notably successful in the competition on constrained single objective real-parameter optimization. Across all considered instances the so-called $\epsilon$MAg-ES achieved the second rank. However, it can be considered to be the most successful participant in high dimensions. Unfortunately, the competition result does not provide any information about the modus operandi of a successful algorithm or its suitability for problems of a particular shape. To this end, the present paper is concerned with an extensive empirical analysis of the $\epsilon$MAg-ES working principles that is expected to provide insights about the performance contribution of specific algorithmic components. To avoid rankings with respect to insignificant differences within the algorithm realizations, the paper additionally introduces significance testing into the ranking process.

Benchmarking Evolutionary Algorithms For Single Objective Real-valued Constrained Optimization - A Critical Review

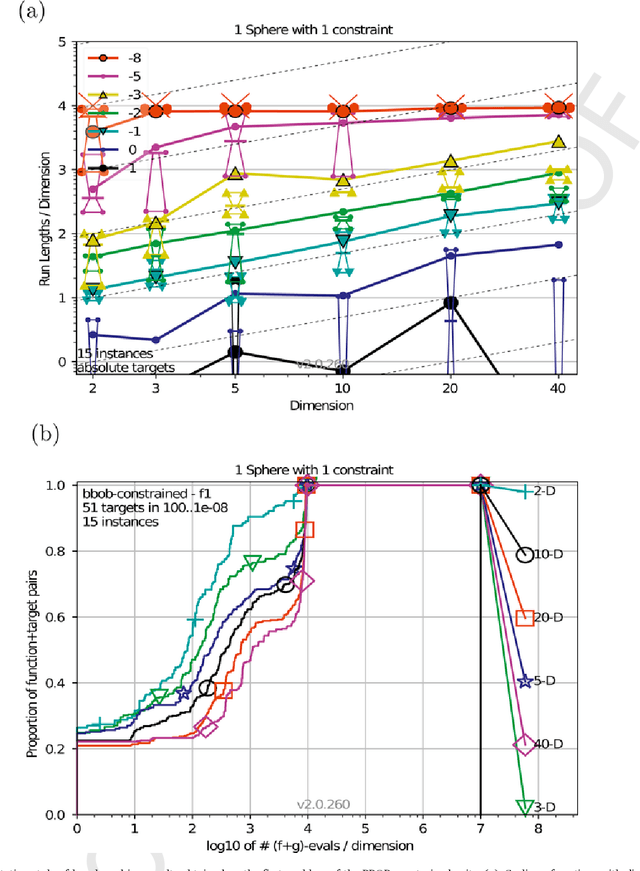
Benchmarking plays an important role in the development of novel search algorithms as well as for the assessment and comparison of contemporary algorithmic ideas. This paper presents common principles that need to be taken into account when considering benchmarking problems for constrained optimization. Current benchmark environments for testing Evolutionary Algorithms are reviewed in the light of these principles. Along with this line, the reader is provided with an overview of the available problem domains in the field of constrained benchmarking. Hence, the review supports algorithms developers with information about the merits and demerits of the available frameworks.

A Covariance Matrix Self-Adaptation Evolution Strategy for Optimization under Linear Constraints

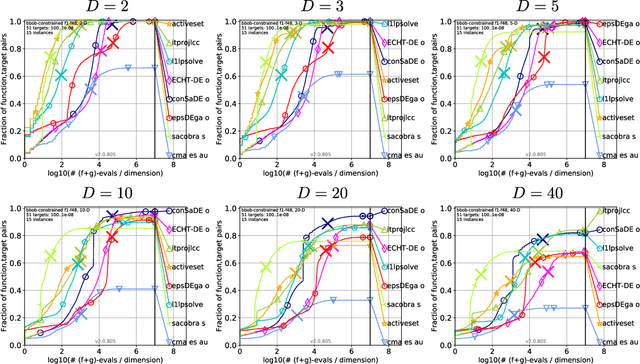
This paper addresses the development of a covariance matrix self-adaptation evolution strategy (CMSA-ES) for solving optimization problems with linear constraints. The proposed algorithm is referred to as Linear Constraint CMSA-ES (lcCMSA-ES). It uses a specially built mutation operator together with repair by projection to satisfy the constraints. The lcCMSA-ES evolves itself on a linear manifold defined by the constraints. The objective function is only evaluated at feasible search points (interior point method). This is a property often required in application domains such as simulation optimization and finite element methods. The algorithm is tested on a variety of different test problems revealing considerable results.

A Linear Constrained Optimization Benchmark For Probabilistic Search Algorithms: The Rotated Klee-Minty Problem

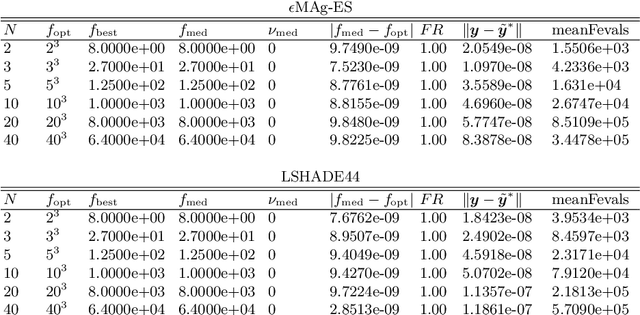
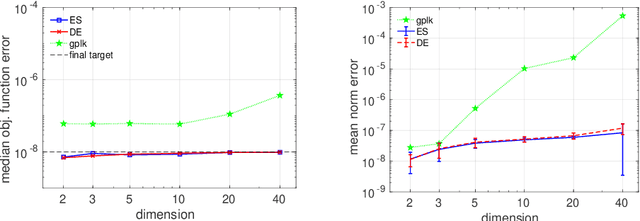
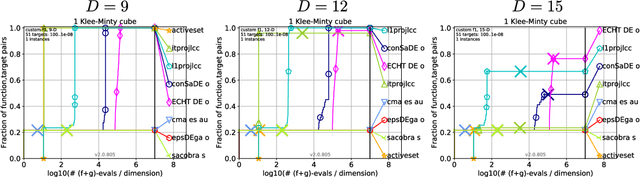
The development, assessment, and comparison of randomized search algorithms heavily rely on benchmarking. Regarding the domain of constrained optimization, the number of currently available benchmark environments bears no relation to the number of distinct problem features. The present paper advances a proposal of a scalable linear constrained optimization problem that is suitable for benchmarking Evolutionary Algorithms. By comparing two recent EA variants, the linear benchmarking environment is demonstrated.