Analysis of the $$-CSA-ES with Repair by Projection Applied to a Conically Constrained Problem

Theoretical analyses of evolution strategies are indispensable for gaining a deep understanding of their inner workings. For constrained problems, rather simple problems are of interest in the current research. This work presents a theoretical analysis of a multi-recombinative evolution strategy with cumulative step size adaptation applied to a conically constrained linear optimization problem. The state of the strategy is modeled by random variables and a stochastic iterative mapping is introduced. For the analytical treatment, fluctuations are neglected and the mean value iterative system is considered. Non-linear difference equations are derived based on one-generation progress rates. Based on that, expressions for the steady state of the mean value iterative system are derived. By comparison with real algorithm runs, it is shown that for the considered assumptions, the theoretical derivations are able to predict the dynamics and the steady state values of the real runs.

Analysis of the $(μ/μ_I,λ)$-$σ$-Self-Adaptation Evolution Strategy with Repair by Projection Applied to a Conically Constrained Problem

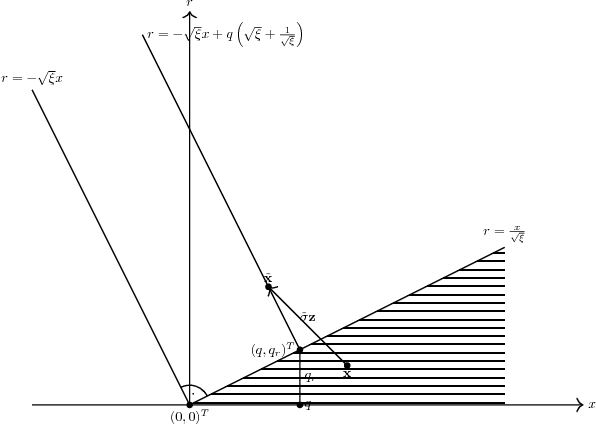
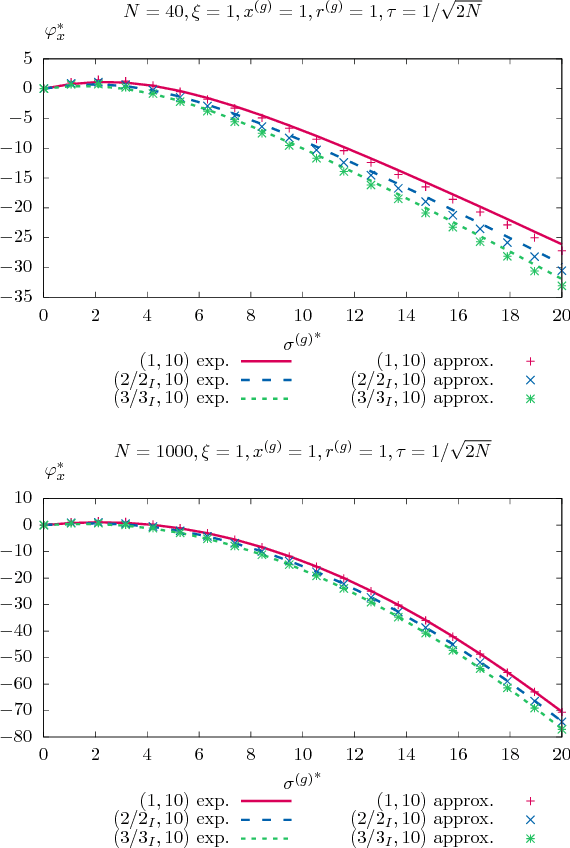
A theoretical performance analysis of the $(\mu/\mu_I,\lambda)$-$\sigma$-Self-Adaptation Evolution Strategy ($\sigma$SA-ES) is presented considering a conically constrained problem. Infeasible offspring are repaired using projection onto the boundary of the feasibility region. Closed-form approximations are used for the one-generation progress of the evolution strategy. Approximate deterministic evolution equations are formulated for analyzing the strategy's dynamics. By iterating the evolution equations with the approximate one-generation expressions, the evolution strategy's dynamics can be predicted. The derived theoretical results are compared to experiments for assessing the approximation quality. It is shown that in the steady state the $(\mu/\mu_I,\lambda)$-$\sigma$SA-ES exhibits a performance as if the ES were optimizing a sphere model. Unlike the non-recombinative $(1,\lambda)$-ES, the parental steady state behavior does not evolve on the cone boundary but stays away from the boundary to a certain extent.

A Covariance Matrix Self-Adaptation Evolution Strategy for Optimization under Linear Constraints

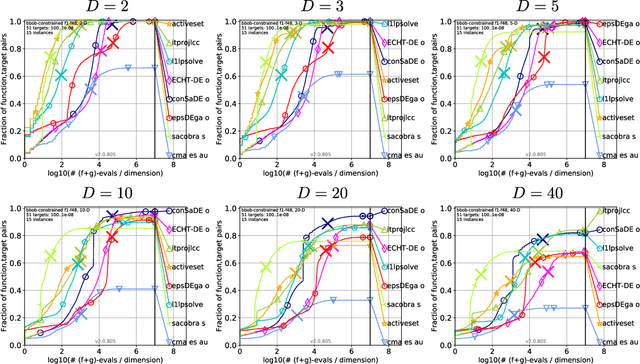
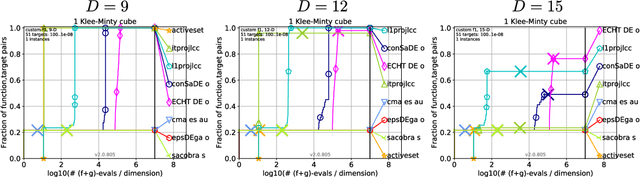
This paper addresses the development of a covariance matrix self-adaptation evolution strategy (CMSA-ES) for solving optimization problems with linear constraints. The proposed algorithm is referred to as Linear Constraint CMSA-ES (lcCMSA-ES). It uses a specially built mutation operator together with repair by projection to satisfy the constraints. The lcCMSA-ES evolves itself on a linear manifold defined by the constraints. The objective function is only evaluated at feasible search points (interior point method). This is a property often required in application domains such as simulation optimization and finite element methods. The algorithm is tested on a variety of different test problems revealing considerable results.