Analysis of the $(μ/μ_I,λ)$-$σ$-Self-Adaptation Evolution Strategy with Repair by Projection Applied to a Conically Constrained Problem

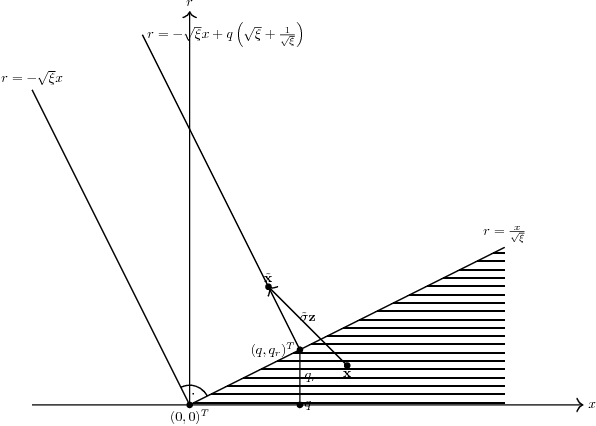
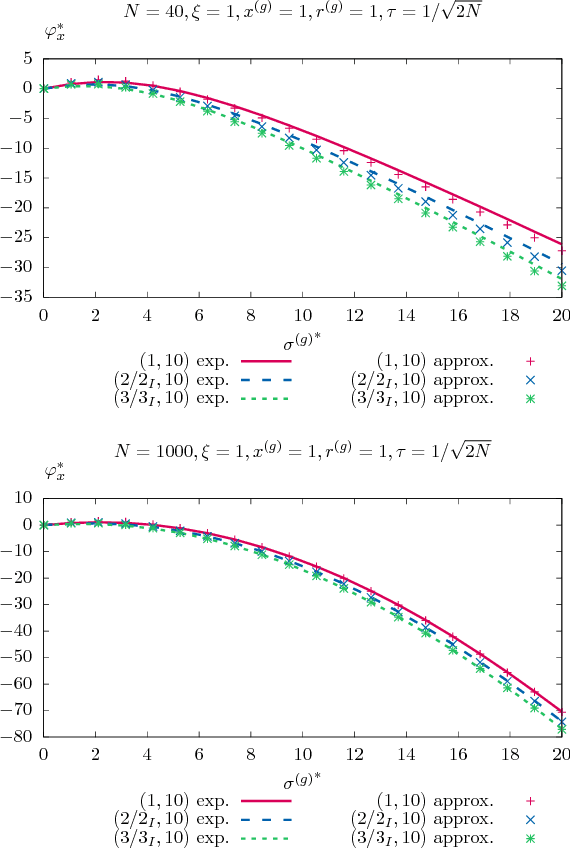
A theoretical performance analysis of the $(\mu/\mu_I,\lambda)$-$\sigma$-Self-Adaptation Evolution Strategy ($\sigma$SA-ES) is presented considering a conically constrained problem. Infeasible offspring are repaired using projection onto the boundary of the feasibility region. Closed-form approximations are used for the one-generation progress of the evolution strategy. Approximate deterministic evolution equations are formulated for analyzing the strategy's dynamics. By iterating the evolution equations with the approximate one-generation expressions, the evolution strategy's dynamics can be predicted. The derived theoretical results are compared to experiments for assessing the approximation quality. It is shown that in the steady state the $(\mu/\mu_I,\lambda)$-$\sigma$SA-ES exhibits a performance as if the ES were optimizing a sphere model. Unlike the non-recombinative $(1,\lambda)$-ES, the parental steady state behavior does not evolve on the cone boundary but stays away from the boundary to a certain extent.