Limited-Memory Matrix Adaptation for Large Scale Black-box Optimization
Paper and Code
May 18, 2017
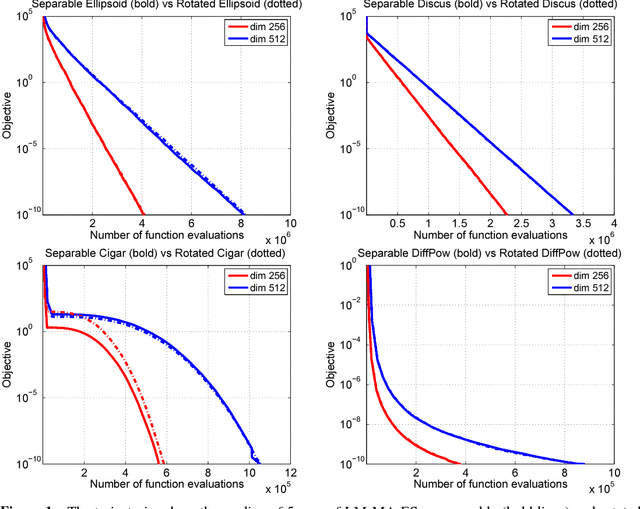
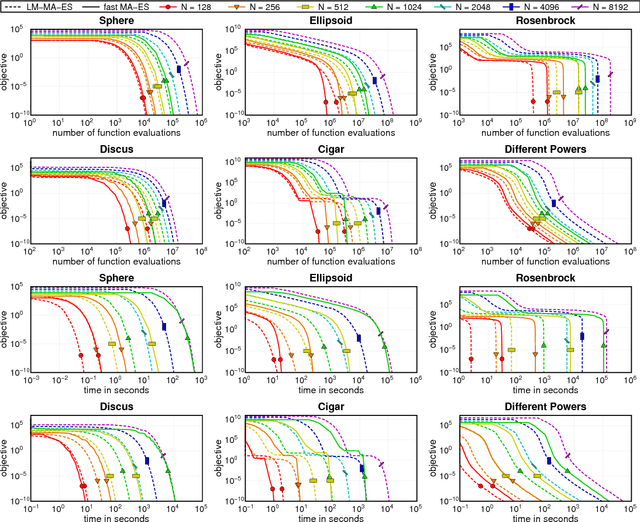
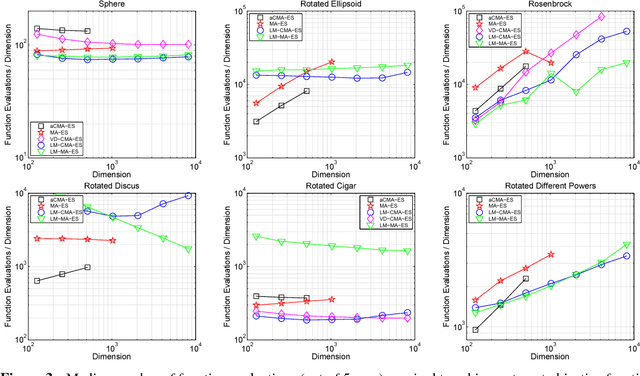
The Covariance Matrix Adaptation Evolution Strategy (CMA-ES) is a popular method to deal with nonconvex and/or stochastic optimization problems when the gradient information is not available. Being based on the CMA-ES, the recently proposed Matrix Adaptation Evolution Strategy (MA-ES) provides a rather surprising result that the covariance matrix and all associated operations (e.g., potentially unstable eigendecomposition) can be replaced in the CMA-ES by a updated transformation matrix without any loss of performance. In order to further simplify MA-ES and reduce its $\mathcal{O}\big(n^2\big)$ time and storage complexity to $\mathcal{O}\big(n\log(n)\big)$, we present the Limited-Memory Matrix Adaptation Evolution Strategy (LM-MA-ES) for efficient zeroth order large-scale optimization. The algorithm demonstrates state-of-the-art performance on a set of established large-scale benchmarks. We explore the algorithm on the problem of generating adversarial inputs for a (non-smooth) random forest classifier, demonstrating a surprising vulnerability of the classifier.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge