NVIDIA Nemotron 3: Efficient and Open Intelligence

We introduce the Nemotron 3 family of models - Nano, Super, and Ultra. These models deliver strong agentic, reasoning, and conversational capabilities. The Nemotron 3 family uses a Mixture-of-Experts hybrid Mamba-Transformer architecture to provide best-in-class throughput and context lengths of up to 1M tokens. Super and Ultra models are trained with NVFP4 and incorporate LatentMoE, a novel approach that improves model quality. The two larger models also include MTP layers for faster text generation. All Nemotron 3 models are post-trained using multi-environment reinforcement learning enabling reasoning, multi-step tool use, and support granular reasoning budget control. Nano, the smallest model, outperforms comparable models in accuracy while remaining extremely cost-efficient for inference. Super is optimized for collaborative agents and high-volume workloads such as IT ticket automation. Ultra, the largest model, provides state-of-the-art accuracy and reasoning performance. Nano is released together with its technical report and this white paper, while Super and Ultra will follow in the coming months. We will openly release the model weights, pre- and post-training software, recipes, and all data for which we hold redistribution rights.

Nemotron 3 Nano: Open, Efficient Mixture-of-Experts Hybrid Mamba-Transformer Model for Agentic Reasoning

We present Nemotron 3 Nano 30B-A3B, a Mixture-of-Experts hybrid Mamba-Transformer language model. Nemotron 3 Nano was pretrained on 25 trillion text tokens, including more than 3 trillion new unique tokens over Nemotron 2, followed by supervised fine tuning and large-scale RL on diverse environments. Nemotron 3 Nano achieves better accuracy than our previous generation Nemotron 2 Nano while activating less than half of the parameters per forward pass. It achieves up to 3.3x higher inference throughput than similarly-sized open models like GPT-OSS-20B and Qwen3-30B-A3B-Thinking-2507, while also being more accurate on popular benchmarks. Nemotron 3 Nano demonstrates enhanced agentic, reasoning, and chat abilities and supports context lengths up to 1M tokens. We release both our pretrained Nemotron 3 Nano 30B-A3B Base and post-trained Nemotron 3 Nano 30B-A3B checkpoints on Hugging Face.

nGPT: Normalized Transformer with Representation Learning on the Hypersphere

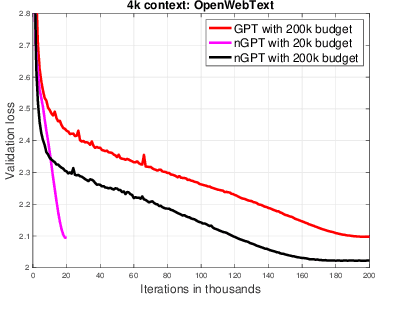
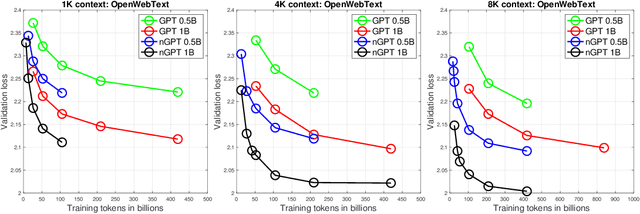
We propose a novel neural network architecture, the normalized Transformer (nGPT) with representation learning on the hypersphere. In nGPT, all vectors forming the embeddings, MLP, attention matrices and hidden states are unit norm normalized. The input stream of tokens travels on the surface of a hypersphere, with each layer contributing a displacement towards the target output predictions. These displacements are defined by the MLP and attention blocks, whose vector components also reside on the same hypersphere. Experiments show that nGPT learns much faster, reducing the number of training steps required to achieve the same accuracy by a factor of 4 to 20, depending on the sequence length.

Weight Norm Control

We note that decoupled weight decay regularization is a particular case of weight norm control where the target norm of weights is set to 0. Any optimization method (e.g., Adam) which uses decoupled weight decay regularization (respectively, AdamW) can be viewed as a particular case of a more general algorithm with weight norm control (respectively, AdamWN). We argue that setting the target norm of weights to 0 can be suboptimal and other target norm values can be considered. For instance, any training run where AdamW achieves a particular norm of weights can be challenged by AdamWN scheduled to achieve a comparable norm of weights. We discuss various implications of introducing weight norm control instead of weight decay.

Back to Basics: Benchmarking Canonical Evolution Strategies for Playing Atari

Evolution Strategies (ES) have recently been demonstrated to be a viable alternative to reinforcement learning (RL) algorithms on a set of challenging deep RL problems, including Atari games and MuJoCo humanoid locomotion benchmarks. While the ES algorithms in that work belonged to the specialized class of natural evolution strategies (which resemble approximate gradient RL algorithms, such as REINFORCE), we demonstrate that even a very basic canonical ES algorithm can achieve the same or even better performance. This success of a basic ES algorithm suggests that the state-of-the-art can be advanced further by integrating the many advances made in the field of ES in the last decades. We also demonstrate qualitatively that ES algorithms have very different performance characteristics than traditional RL algorithms: on some games, they learn to exploit the environment and perform much better while on others they can get stuck in suboptimal local minima. Combining their strengths with those of traditional RL algorithms is therefore likely to lead to new advances in the state of the art.

Fixing Weight Decay Regularization in Adam

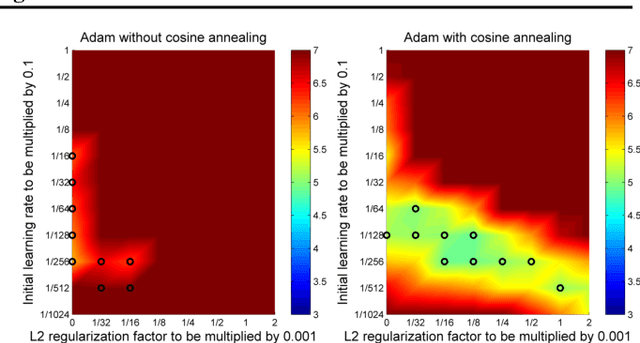
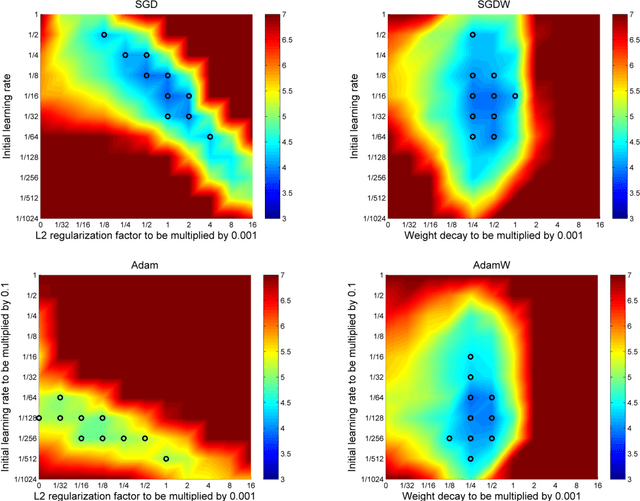
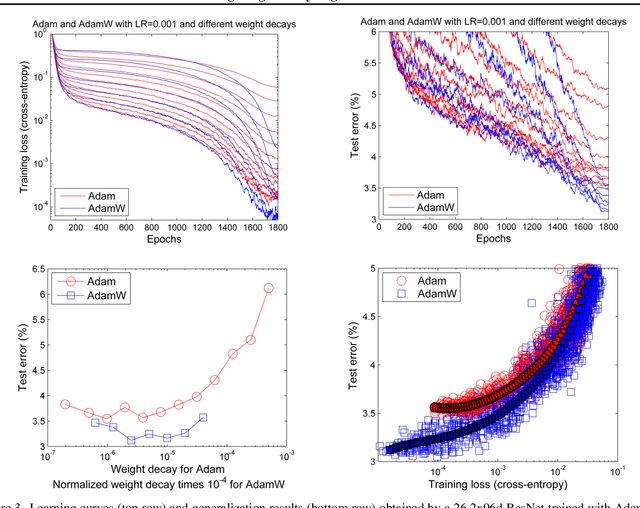
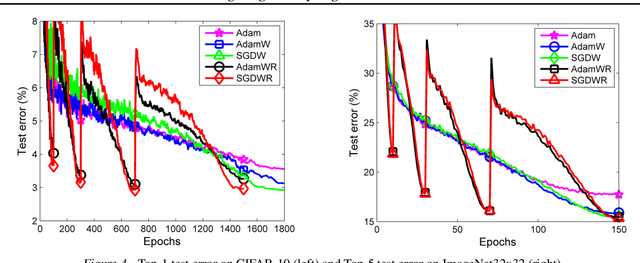
L$_2$ regularization and weight decay regularization are equivalent for standard stochastic gradient descent (when rescaled by the learning rate), but as we demonstrate this is \emph{not} the case for adaptive gradient algorithms, such as Adam. While common deep learning frameworks of these algorithms implement L$_2$ regularization (often calling it "weight decay" in what may be misleading due to the inequivalence we expose), we propose a simple modification to recover the original formulation of weight decay regularization by decoupling the weight decay from the optimization steps taken w.r.t. the loss function. We provide empirical evidence that our proposed modification (i) decouples the optimal choice of weight decay factor from the setting of the learning rate for both standard SGD and Adam, and (ii) substantially improves Adam's generalization performance, allowing it to compete with SGD with momentum on image classification datasets (on which it was previously typically outperformed by the latter). We also propose a version of Adam with warm restarts (AdamWR) that has strong anytime performance while achieving state-of-the-art results on CIFAR-10 and ImageNet32x32. Our source code is available at https://github.com/loshchil/AdamW-and-SGDW

A Downsampled Variant of ImageNet as an Alternative to the CIFAR datasets

The original ImageNet dataset is a popular large-scale benchmark for training Deep Neural Networks. Since the cost of performing experiments (e.g, algorithm design, architecture search, and hyperparameter tuning) on the original dataset might be prohibitive, we propose to consider a downsampled version of ImageNet. In contrast to the CIFAR datasets and earlier downsampled versions of ImageNet, our proposed ImageNet32$\times$32 (and its variants ImageNet64$\times$64 and ImageNet16$\times$16) contains exactly the same number of classes and images as ImageNet, with the only difference that the images are downsampled to 32$\times$32 pixels per image (64$\times$64 and 16$\times$16 pixels for the variants, respectively). Experiments on these downsampled variants are dramatically faster than on the original ImageNet and the characteristics of the downsampled datasets with respect to optimal hyperparameters appear to remain similar. The proposed datasets and scripts to reproduce our results are available at http://image-net.org/download-images and https://github.com/PatrykChrabaszcz/Imagenet32_Scripts

Limited-Memory Matrix Adaptation for Large Scale Black-box Optimization

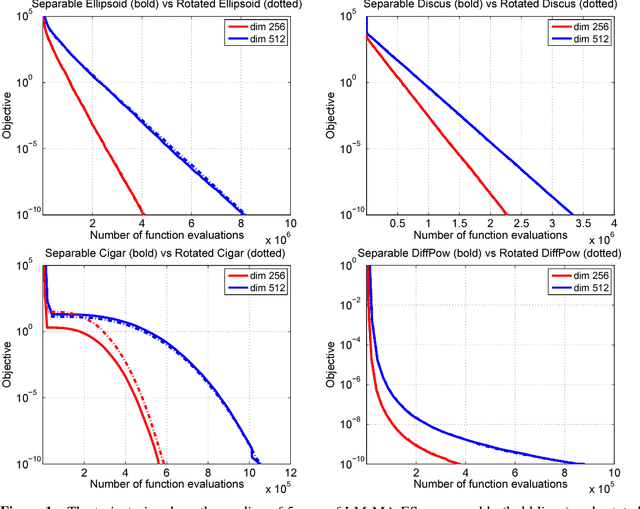
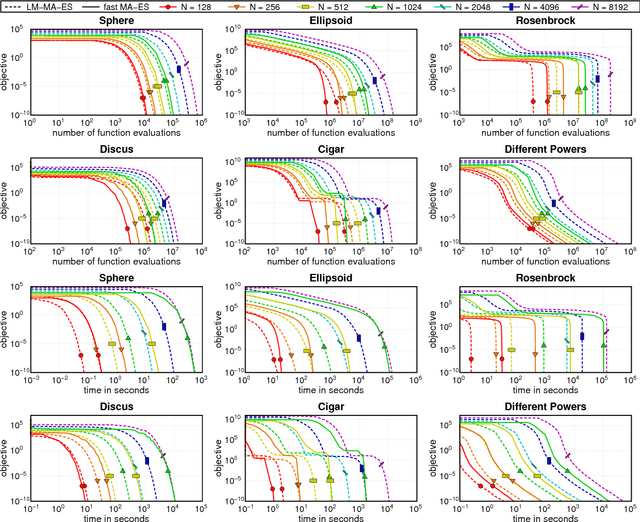
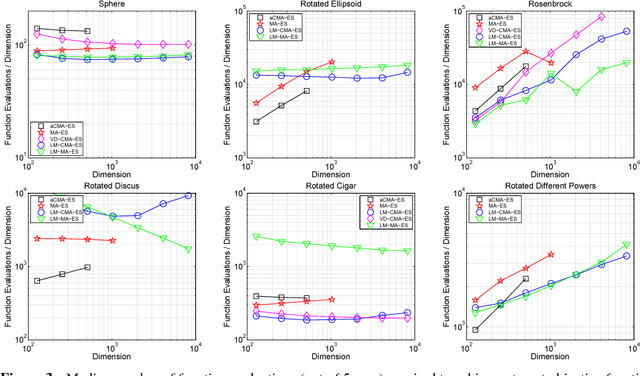
The Covariance Matrix Adaptation Evolution Strategy (CMA-ES) is a popular method to deal with nonconvex and/or stochastic optimization problems when the gradient information is not available. Being based on the CMA-ES, the recently proposed Matrix Adaptation Evolution Strategy (MA-ES) provides a rather surprising result that the covariance matrix and all associated operations (e.g., potentially unstable eigendecomposition) can be replaced in the CMA-ES by a updated transformation matrix without any loss of performance. In order to further simplify MA-ES and reduce its $\mathcal{O}\big(n^2\big)$ time and storage complexity to $\mathcal{O}\big(n\log(n)\big)$, we present the Limited-Memory Matrix Adaptation Evolution Strategy (LM-MA-ES) for efficient zeroth order large-scale optimization. The algorithm demonstrates state-of-the-art performance on a set of established large-scale benchmarks. We explore the algorithm on the problem of generating adversarial inputs for a (non-smooth) random forest classifier, demonstrating a surprising vulnerability of the classifier.

SGDR: Stochastic Gradient Descent with Warm Restarts

Restart techniques are common in gradient-free optimization to deal with multimodal functions. Partial warm restarts are also gaining popularity in gradient-based optimization to improve the rate of convergence in accelerated gradient schemes to deal with ill-conditioned functions. In this paper, we propose a simple warm restart technique for stochastic gradient descent to improve its anytime performance when training deep neural networks. We empirically study its performance on the CIFAR-10 and CIFAR-100 datasets, where we demonstrate new state-of-the-art results at 3.14% and 16.21%, respectively. We also demonstrate its advantages on a dataset of EEG recordings and on a downsampled version of the ImageNet dataset. Our source code is available at https://github.com/loshchil/SGDR

Anytime Bi-Objective Optimization with a Hybrid Multi-Objective CMA-ES (HMO-CMA-ES)

We propose a multi-objective optimization algorithm aimed at achieving good anytime performance over a wide range of problems. Performance is assessed in terms of the hypervolume metric. The algorithm called HMO-CMA-ES represents a hybrid of several old and new variants of CMA-ES, complemented by BOBYQA as a warm start. We benchmark HMO-CMA-ES on the recently introduced bi-objective problem suite of the COCO framework (COmparing Continuous Optimizers), consisting of 55 scalable continuous optimization problems, which is used by the Black-Box Optimization Benchmarking (BBOB) Workshop 2016.