Fixing Weight Decay Regularization in Adam
Paper and Code
Feb 14, 2018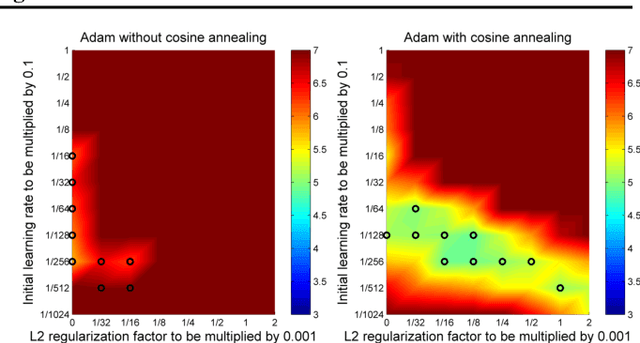
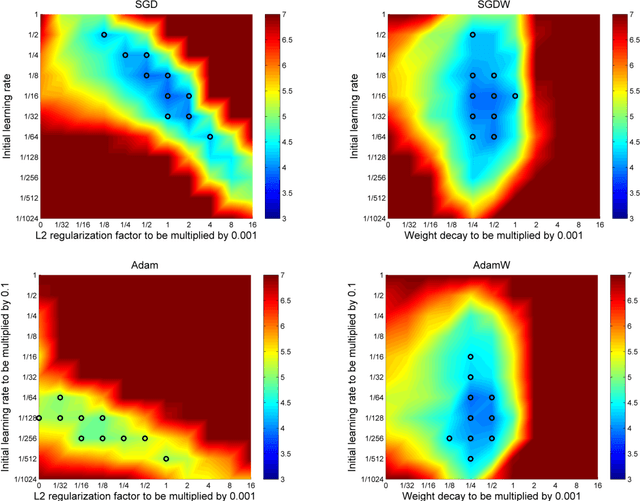
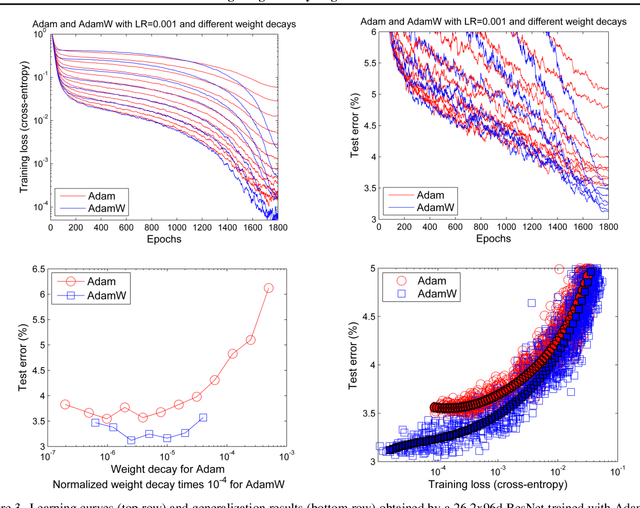
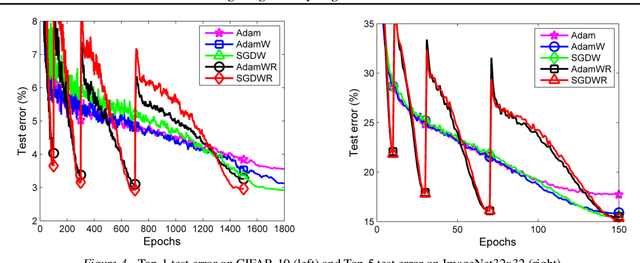
L$_2$ regularization and weight decay regularization are equivalent for standard stochastic gradient descent (when rescaled by the learning rate), but as we demonstrate this is \emph{not} the case for adaptive gradient algorithms, such as Adam. While common deep learning frameworks of these algorithms implement L$_2$ regularization (often calling it "weight decay" in what may be misleading due to the inequivalence we expose), we propose a simple modification to recover the original formulation of weight decay regularization by decoupling the weight decay from the optimization steps taken w.r.t. the loss function. We provide empirical evidence that our proposed modification (i) decouples the optimal choice of weight decay factor from the setting of the learning rate for both standard SGD and Adam, and (ii) substantially improves Adam's generalization performance, allowing it to compete with SGD with momentum on image classification datasets (on which it was previously typically outperformed by the latter). We also propose a version of Adam with warm restarts (AdamWR) that has strong anytime performance while achieving state-of-the-art results on CIFAR-10 and ImageNet32x32. Our source code is available at https://github.com/loshchil/AdamW-and-SGDW
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge