Domaino1s: Guiding LLM Reasoning for Explainable Answers in High-Stakes Domains

Large Language Models (LLMs) are widely applied to downstream domains. However, current LLMs for high-stakes domain tasks, such as financial investment and legal QA, typically generate brief answers without reasoning processes and explanations. This limits users' confidence in making decisions based on their responses. While original CoT shows promise, it lacks self-correction mechanisms during reasoning. This work introduces Domain$o1$s, which enhances LLMs' reasoning capabilities on domain tasks through supervised fine-tuning and tree search. We construct CoT-stock-2k and CoT-legal-2k datasets for fine-tuning models that activate domain-specific reasoning steps based on their judgment. Additionally, we propose Selective Tree Exploration to spontaneously explore solution spaces and sample optimal reasoning paths to improve performance. We also introduce PROOF-Score, a new metric for evaluating domain models' explainability, complementing traditional accuracy metrics with richer assessment dimensions. Extensive experiments on stock investment recommendation and legal reasoning QA tasks demonstrate Domaino1s's leading performance and explainability. Our code is available at https://anonymous.4open.science/r/Domaino1s-006F/.

GraphBC: Improving LLMs for Better Graph Data Processing

The success of Large Language Models (LLMs) in various domains has led researchers to apply them to graph-related problems by converting graph data into natural language text. However, unlike graph data, natural language inherently has sequential order. We observe that when the order of nodes or edges in the natural language description of a graph is shuffled, despite describing the same graph, model performance fluctuates between high performance and random guessing. Additionally, due to the limited input context length of LLMs, current methods typically randomly sample neighbors of target nodes as representatives of their neighborhood, which may not always be effective for accurate reasoning. To address these gaps, we introduce GraphBC. This novel model framework features an Order Selector Module to ensure proper serialization order of the graph and a Subgraph Sampling Module to sample subgraphs with better structure for better reasoning. Furthermore, we propose Graph CoT obtained through distillation, and enhance LLM's reasoning and zero-shot learning capabilities for graph tasks through instruction tuning. Experiments on multiple datasets for node classification and graph question-answering demonstrate that GraphBC improves LLMs' performance and generalization ability on graph tasks.

Adaptive Spatiotemporal Augmentation for Improving Dynamic Graph Learning

Dynamic graph augmentation is used to improve the performance of dynamic GNNs. Most methods assume temporal locality, meaning that recent edges are more influential than earlier edges. However, for temporal changes in edges caused by random noise, overemphasizing recent edges while neglecting earlier ones may lead to the model capturing noise. To address this issue, we propose STAA (SpatioTemporal Activity-Aware Random Walk Diffusion). STAA identifies nodes likely to have noisy edges in spatiotemporal dimensions. Spatially, it analyzes critical topological positions through graph wavelet coefficients. Temporally, it analyzes edge evolution through graph wavelet coefficient change rates. Then, random walks are used to reduce the weights of noisy edges, deriving a diffusion matrix containing spatiotemporal information as an augmented adjacency matrix for dynamic GNN learning. Experiments on multiple datasets show that STAA outperforms other dynamic graph augmentation methods in node classification and link prediction tasks.

Total Variation and Euler's Elastica for Supervised Learning

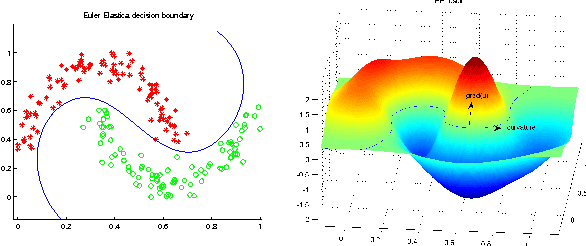
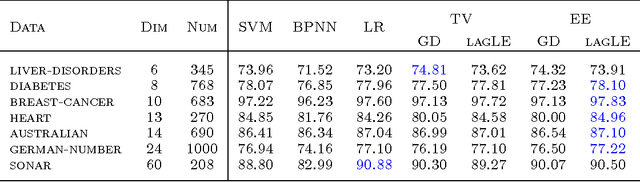
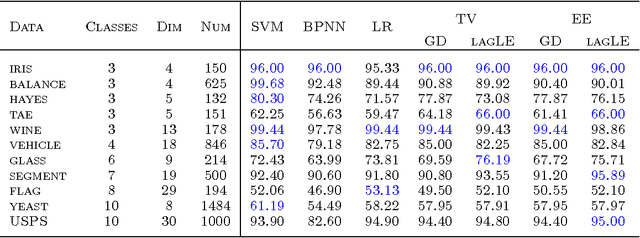
In recent years, total variation (TV) and Euler's elastica (EE) have been successfully applied to image processing tasks such as denoising and inpainting. This paper investigates how to extend TV and EE to the supervised learning settings on high dimensional data. The supervised learning problem can be formulated as an energy functional minimization under Tikhonov regularization scheme, where the energy is composed of a squared loss and a total variation smoothing (or Euler's elastica smoothing). Its solution via variational principles leads to an Euler-Lagrange PDE. However, the PDE is always high-dimensional and cannot be directly solved by common methods. Instead, radial basis functions are utilized to approximate the target function, reducing the problem to finding the linear coefficients of basis functions. We apply the proposed methods to supervised learning tasks (including binary classification, multi-class classification, and regression) on benchmark data sets. Extensive experiments have demonstrated promising results of the proposed methods.