Few is More: Task-Efficient Skill-Discovery for Multi-Task Offline Multi-Agent Reinforcement Learning

As a data-driven approach, offline MARL learns superior policies solely from offline datasets, ideal for domains rich in historical data but with high interaction costs and risks. However, most existing methods are task-specific, requiring retraining for new tasks, leading to redundancy and inefficiency. To address this issue, in this paper, we propose a task-efficient multi-task offline MARL algorithm, Skill-Discovery Conservative Q-Learning (SD-CQL). Unlike existing offline skill-discovery methods, SD-CQL discovers skills by reconstructing the next observation. It then evaluates fixed and variable actions separately and employs behavior-regularized conservative Q-learning to execute the optimal action for each skill. This approach eliminates the need for local-global alignment and enables strong multi-task generalization from limited small-scale source tasks. Substantial experiments on StarCraftII demonstrates the superior generalization performance and task-efficiency of SD-CQL. It achieves the best performance on $\textbf{10}$ out of $14$ task sets, with up to $\textbf{65%}$ improvement on individual task sets, and is within $4\%$ of the best baseline on the remaining four.

Offline-to-Online Multi-Agent Reinforcement Learning with Offline Value Function Memory and Sequential Exploration

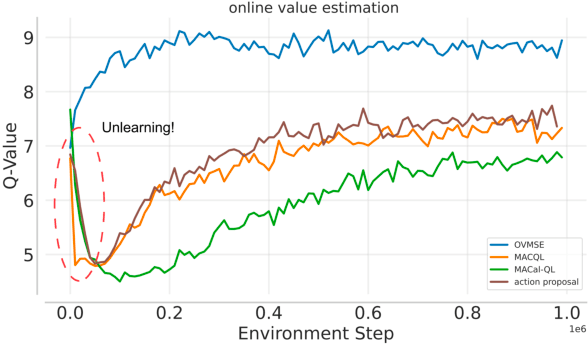
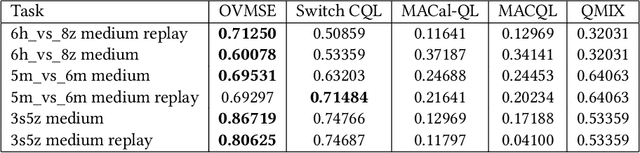
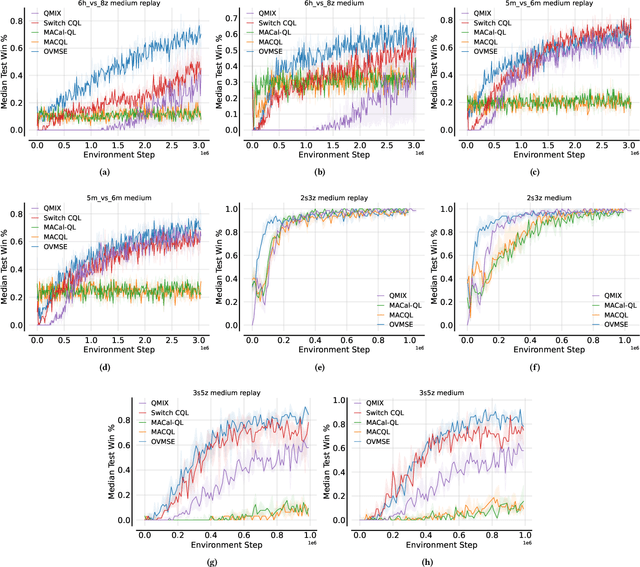
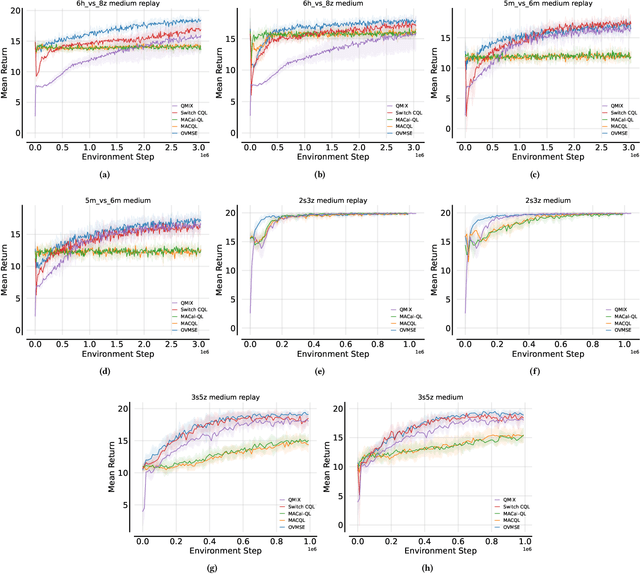
Offline-to-Online Reinforcement Learning has emerged as a powerful paradigm, leveraging offline data for initialization and online fine-tuning to enhance both sample efficiency and performance. However, most existing research has focused on single-agent settings, with limited exploration of the multi-agent extension, i.e., Offline-to-Online Multi-Agent Reinforcement Learning (O2O MARL). In O2O MARL, two critical challenges become more prominent as the number of agents increases: (i) the risk of unlearning pre-trained Q-values due to distributional shifts during the transition from offline-to-online phases, and (ii) the difficulty of efficient exploration in the large joint state-action space. To tackle these challenges, we propose a novel O2O MARL framework called Offline Value Function Memory with Sequential Exploration (OVMSE). First, we introduce the Offline Value Function Memory (OVM) mechanism to compute target Q-values, preserving knowledge gained during offline training, ensuring smoother transitions, and enabling efficient fine-tuning. Second, we propose a decentralized Sequential Exploration (SE) strategy tailored for O2O MARL, which effectively utilizes the pre-trained offline policy for exploration, thereby significantly reducing the joint state-action space to be explored. Extensive experiments on the StarCraft Multi-Agent Challenge (SMAC) demonstrate that OVMSE significantly outperforms existing baselines, achieving superior sample efficiency and overall performance.

Chance-Constrained Iterative Linear-Quadratic Stochastic Games

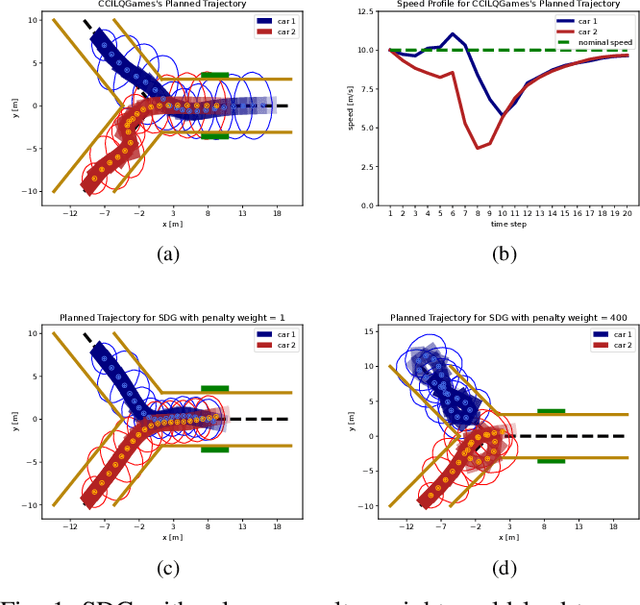
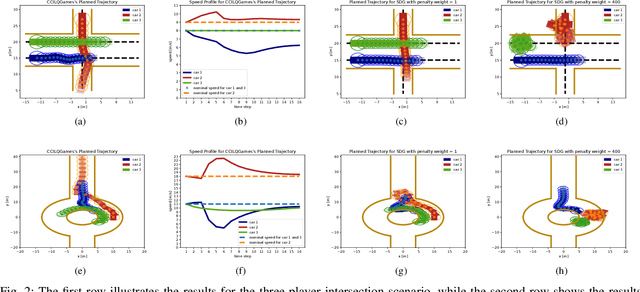
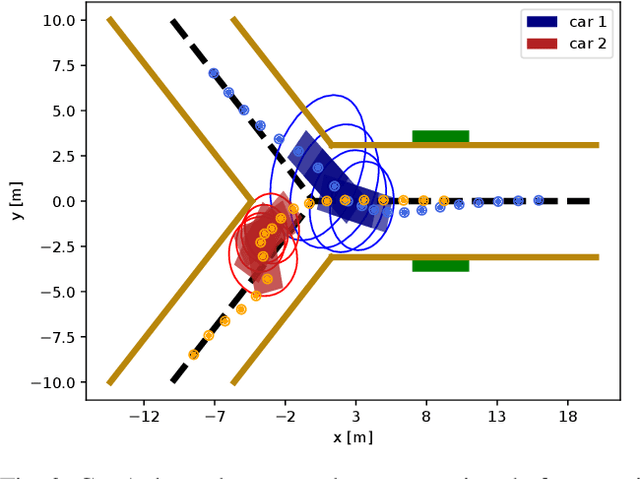
Dynamic game arises as a powerful paradigm for multi-robot planning, for which the safety constraints satisfaction is crucial. Constrained stochastic games are of particular interest, as real-world robots need to operate and satisfy constraints under uncertainty. Existing methods for solving stochastic games handle constraints using soft penalties with hand-tuned weights. However, finding a suitable penalty weight is non-trivial and requires trial and error. In this paper, we propose the chance-constrained iterative linear-quadratic stochastic games (CCILQGames) algorithm. CCILQGames solves chance-constrained stochastic games using the augmented Lagrangian method, with the merit of automatically finding a suitable penalty weight. We evaluate our algorithm in three autonomous driving scenarios, including merge, intersection, and roundabout. Experimental results and Monte Carlo tests show that CCILQGames could generate safe and interactive strategies in stochastic environments.