FairSort: Learning to Fair Rank for Personalized Recommendations in Two-Sided Platforms

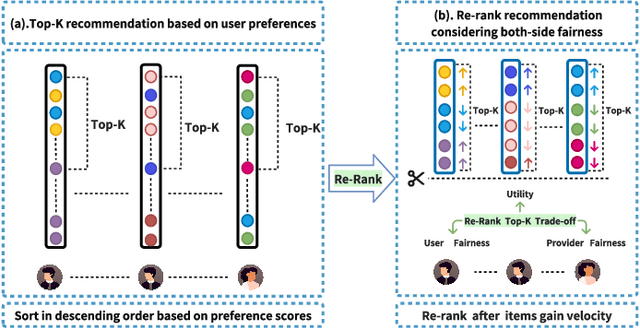
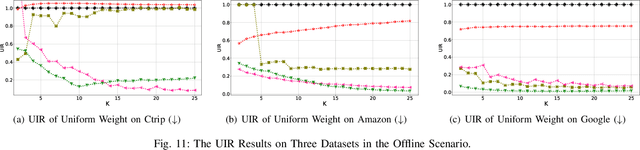
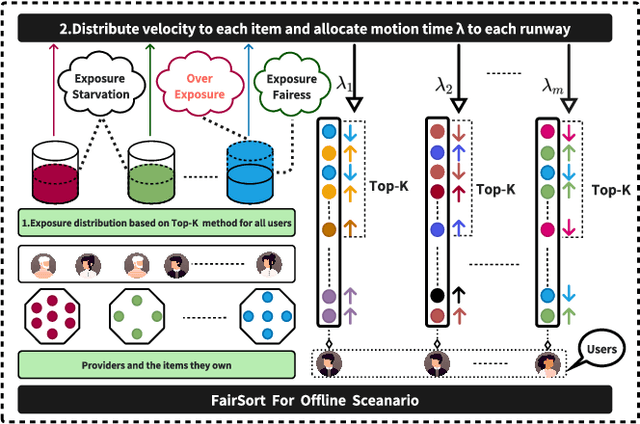
Traditional recommendation systems focus on maximizing user satisfaction by suggesting their favorite items. This user-centric approach may lead to unfair exposure distribution among the providers. On the contrary, a provider-centric design might become unfair to the users. Therefore, this paper proposes a re-ranking model FairSort\footnote{\textbf{Reproducibility:}The code and datasets are available at \url{https://github.com/13543024276/FairSort}} to find a trade-off solution among user-side fairness, provider-side fairness, and personalized recommendations utility. Previous works habitually treat this issue as a knapsack problem, incorporating both-side fairness as constraints. In this paper, we adopt a novel perspective, treating each recommendation list as a runway rather than a knapsack. In this perspective, each item on the runway gains a velocity and runs within a specific time, achieving re-ranking for both-side fairness. Meanwhile, we ensure the Minimum Utility Guarantee for personalized recommendations by designing a Binary Search approach. This can provide more reliable recommendations compared to the conventional greedy strategy based on the knapsack problem. We further broaden the applicability of FairSort, designing two versions for online and offline recommendation scenarios. Theoretical analysis and extensive experiments on real-world datasets indicate that FairSort can ensure more reliable personalized recommendations while considering fairness for both the provider and user.

Bayesian geoacoustic inversion using mixture density network

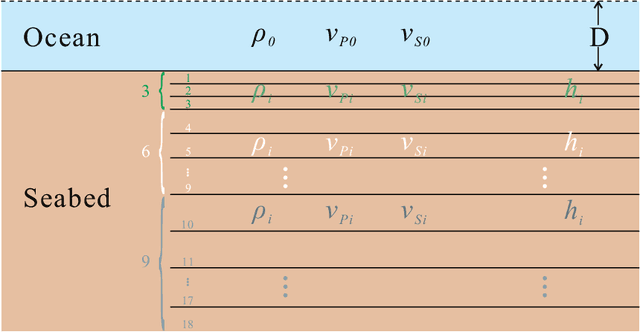
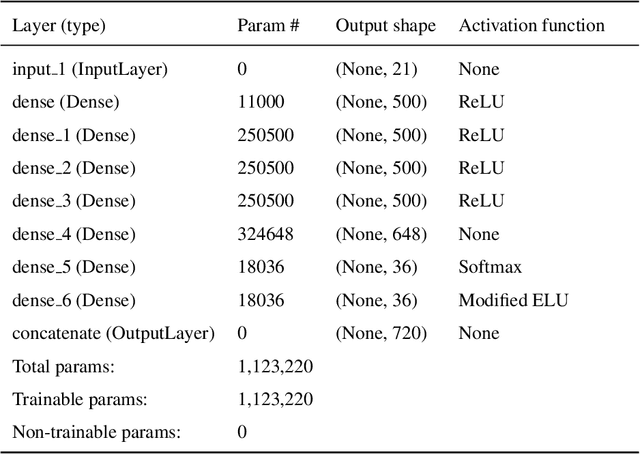
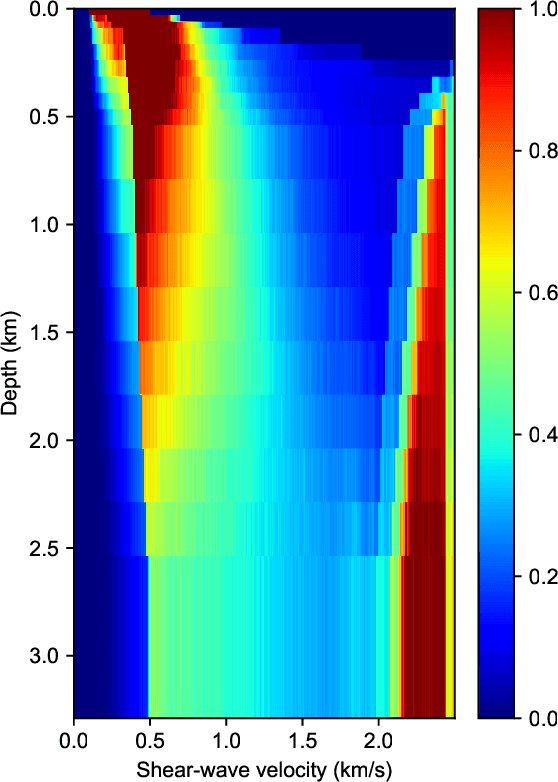
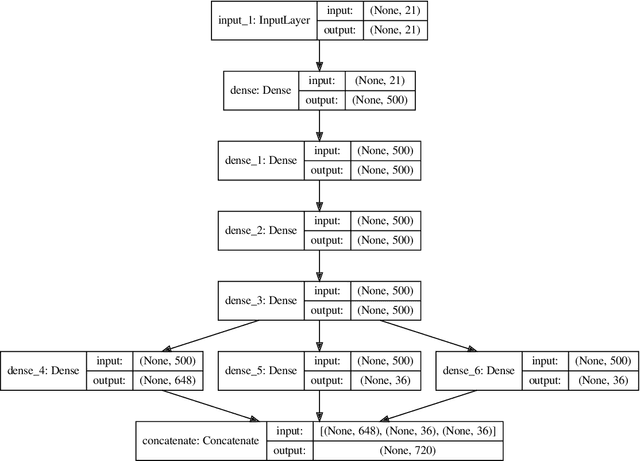
Bayesian geoacoustic inversion problems are conventionally solved by Markov chain Monte Carlo methods or its variants, which are computationally expensive. This paper extends the classic Bayesian geoacoustic inversion framework using the mixture density network (MDN), which provides a much more efficient way to solve geoacoustic inversion problems in Bayesian inference framework. Some important geoacoustic statistics of Bayesian geoacoustic inversion are derived from the multidimensional posterior probability density (PPD) using the MDN theory. These statistics make it convenient to train the network directly on the whole parameter space and get the multidimensional PPD of model parameters. The network is trained on a simulated dataset of surface-wave dispersion curves with shear-wave velocities as labels. The results show that the network gives reliable predictions and has good generalization performance on unseen data. Once trained, the network can rapidly (within seconds) give a fully probabilistic solution which is comparable to Monte Carlo methods. It provides an promissing approach for real-time inversion.