Long-Term Prediction Accuracy Improvement of Data-Driven Medium-Range Global Weather Forecast

Long-term stability stands as a crucial requirement in data-driven medium-range global weather forecasting. Spectral bias is recognized as the primary contributor to instabilities, as data-driven methods difficult to learn small-scale dynamics. In this paper, we reveal that the universal mechanism for these instabilities is not only related to spectral bias but also to distortions brought by processing spherical data using conventional convolution. These distortions lead to a rapid amplification of errors over successive long-term iterations, resulting in a significant decline in forecast accuracy. To address this issue, a universal neural operator called the Spherical Harmonic Neural Operator (SHNO) is introduced to improve long-term iterative forecasts. SHNO uses the spherical harmonic basis to mitigate distortions for spherical data and uses gated residual spectral attention (GRSA) to correct spectral bias caused by spurious correlations across different scales. The effectiveness and merit of the proposed method have been validated through its application for spherical Shallow Water Equations (SWEs) and medium-range global weather forecasting. Our findings highlight the benefits and potential of SHNO to improve the accuracy of long-term prediction.

Bayesian geoacoustic inversion using mixture density network

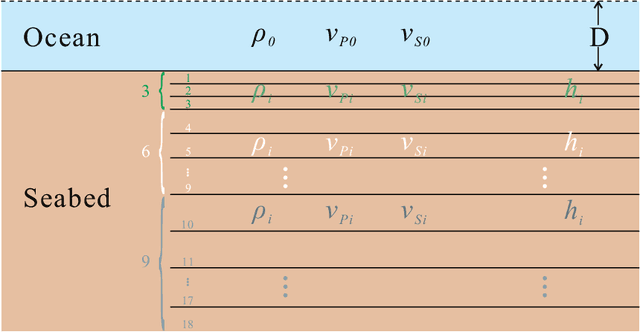
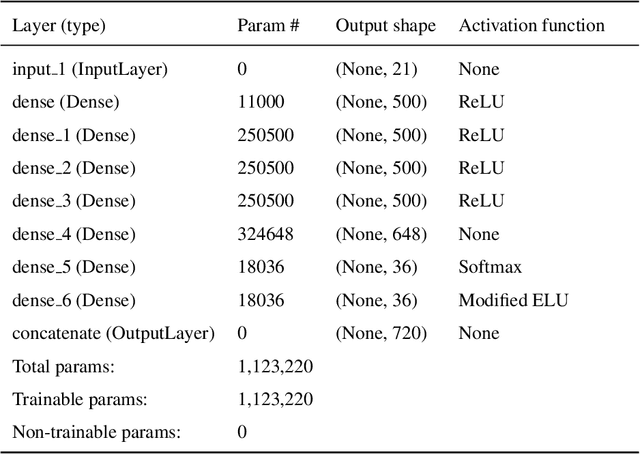
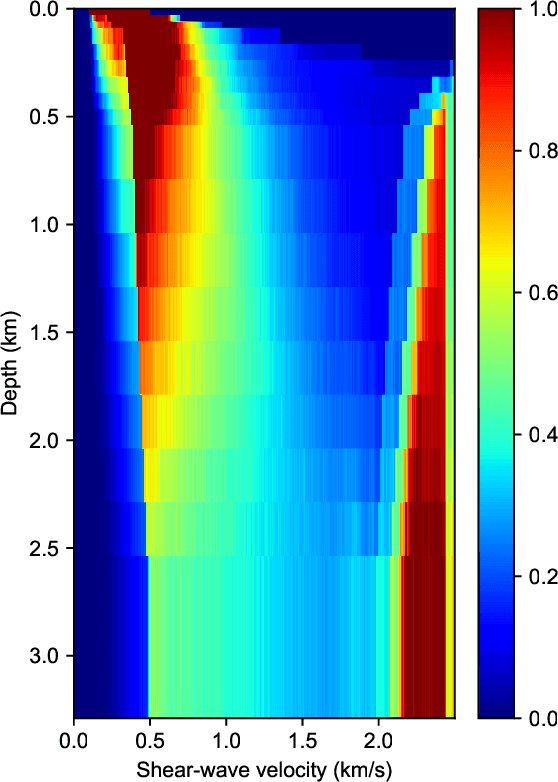
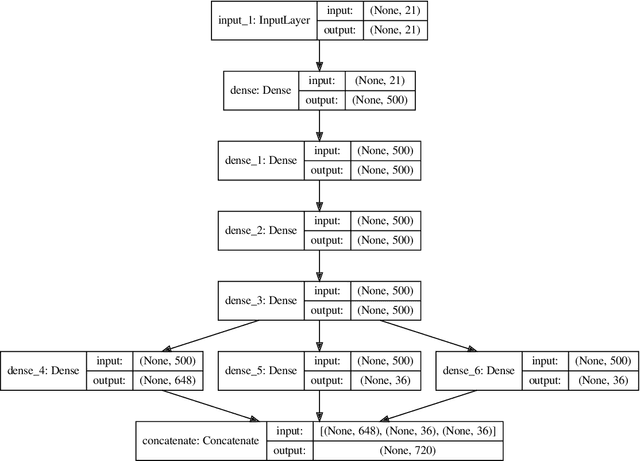
Bayesian geoacoustic inversion problems are conventionally solved by Markov chain Monte Carlo methods or its variants, which are computationally expensive. This paper extends the classic Bayesian geoacoustic inversion framework using the mixture density network (MDN), which provides a much more efficient way to solve geoacoustic inversion problems in Bayesian inference framework. Some important geoacoustic statistics of Bayesian geoacoustic inversion are derived from the multidimensional posterior probability density (PPD) using the MDN theory. These statistics make it convenient to train the network directly on the whole parameter space and get the multidimensional PPD of model parameters. The network is trained on a simulated dataset of surface-wave dispersion curves with shear-wave velocities as labels. The results show that the network gives reliable predictions and has good generalization performance on unseen data. Once trained, the network can rapidly (within seconds) give a fully probabilistic solution which is comparable to Monte Carlo methods. It provides an promissing approach for real-time inversion.