Core Knowledge Learning Framework for Graph Adaptation and Scalability Learning

Graph classification is a pivotal challenge in machine learning, especially within the realm of graph-based data, given its importance in numerous real-world applications such as social network analysis, recommendation systems, and bioinformatics. Despite its significance, graph classification faces several hurdles, including adapting to diverse prediction tasks, training across multiple target domains, and handling small-sample prediction scenarios. Current methods often tackle these challenges individually, leading to fragmented solutions that lack a holistic approach to the overarching problem. In this paper, we propose an algorithm aimed at addressing the aforementioned challenges. By incorporating insights from various types of tasks, our method aims to enhance adaptability, scalability, and generalizability in graph classification. Motivated by the recognition that the underlying subgraph plays a crucial role in GNN prediction, while the remainder is task-irrelevant, we introduce the Core Knowledge Learning (\method{}) framework for graph adaptation and scalability learning. \method{} comprises several key modules, including the core subgraph knowledge submodule, graph domain adaptation module, and few-shot learning module for downstream tasks. Each module is tailored to tackle specific challenges in graph classification, such as domain shift, label inconsistencies, and data scarcity. By learning the core subgraph of the entire graph, we focus on the most pertinent features for task relevance. Consequently, our method offers benefits such as improved model performance, increased domain adaptability, and enhanced robustness to domain variations. Experimental results demonstrate significant performance enhancements achieved by our method compared to state-of-the-art approaches.

EDDA: A Encoder-Decoder Data Augmentation Framework for Zero-Shot Stance Detection

Stance detection aims to determine the attitude expressed in text towards a given target. Zero-shot stance detection (ZSSD) has emerged to classify stances towards unseen targets during inference. Recent data augmentation techniques for ZSSD increase transferable knowledge between targets through text or target augmentation. However, these methods exhibit limitations. Target augmentation lacks logical connections between generated targets and source text, while text augmentation relies solely on training data, resulting in insufficient generalization. To address these issues, we propose an encoder-decoder data augmentation (EDDA) framework. The encoder leverages large language models and chain-of-thought prompting to summarize texts into target-specific if-then rationales, establishing logical relationships. The decoder generates new samples based on these expressions using a semantic correlation word replacement strategy to increase syntactic diversity. We also analyze the generated expressions to develop a rationale-enhanced network that fully utilizes the augmented data. Experiments on benchmark datasets demonstrate our approach substantially improves over state-of-the-art ZSSD techniques. The proposed EDDA framework increases semantic relevance and syntactic variety in augmented texts while enabling interpretable rationale-based learning.

Active-set algorithms based statistical inference for shape-restricted generalized additive Cox regression models

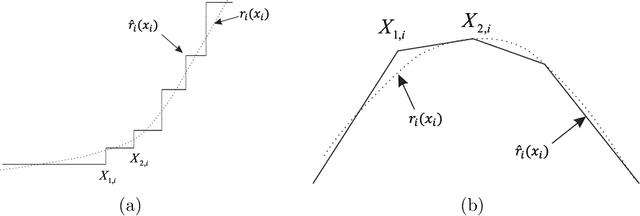
Recently the shape-restricted inference has gained popularity in statistical and econometric literature in order to relax the linear or quadratic covariate effect in regression analyses. The typical shape-restricted covariate effect includes monotonic increasing, decreasing, convexity or concavity. In this paper, we introduce the shape-restricted inference to the celebrated Cox regression model (SR-Cox), in which the covariate response is modeled as shape-restricted additive functions. The SR-Cox regression approximates the shape-restricted functions using a spline basis expansion with data driven choice of knots. The underlying minimization of negative log-likelihood function is formulated as a convex optimization problem, which is solved with an active-set optimization algorithm. The highlight of this algorithm is that it eliminates the superfluous knots automatically. When covariate effects include combinations of convex or concave terms with unknown forms and linear terms, the most interesting finding is that SR-Cox produces accurate linear covariate effect estimates which are comparable to the maximum partial likelihood estimates if indeed the forms are known. We conclude that concave or convex SR-Cox models could significantly improve nonlinear covariate response recovery and model goodness of fit.