Query DAGs: A Practical Paradigm for Implementing Belief Network Inference

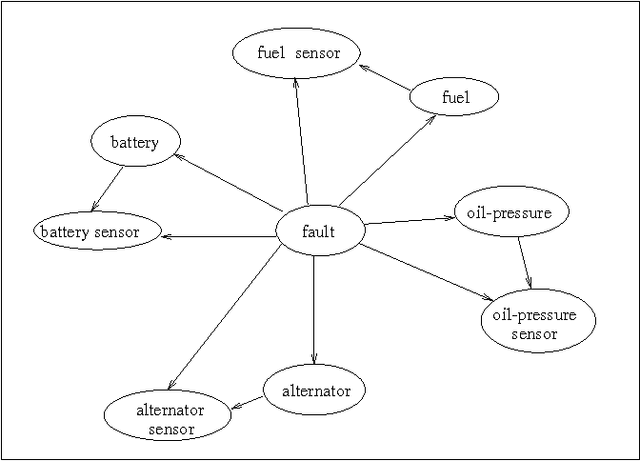
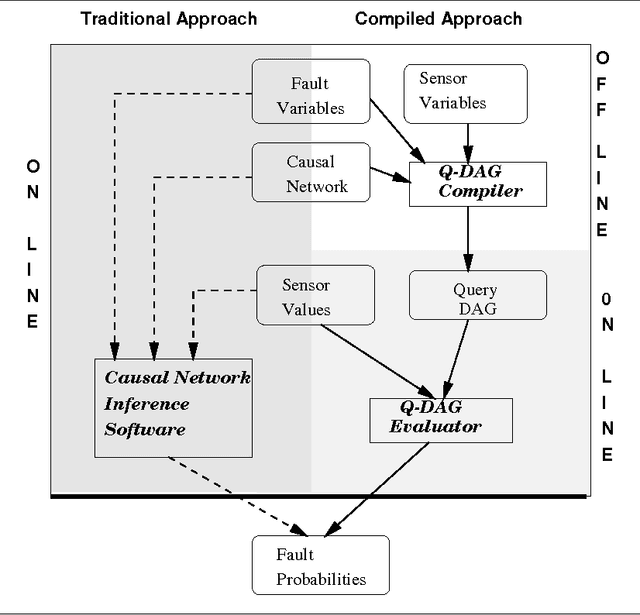
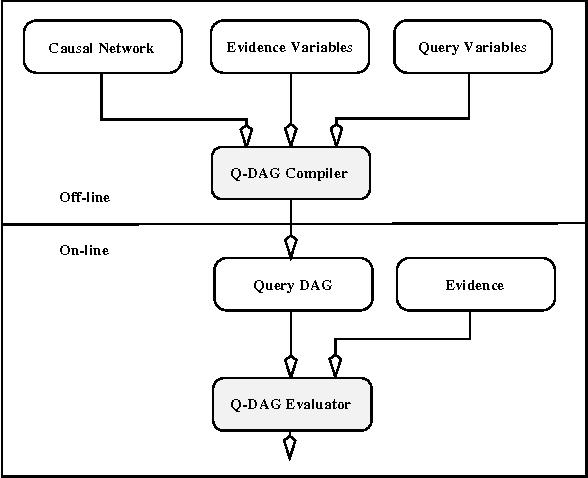
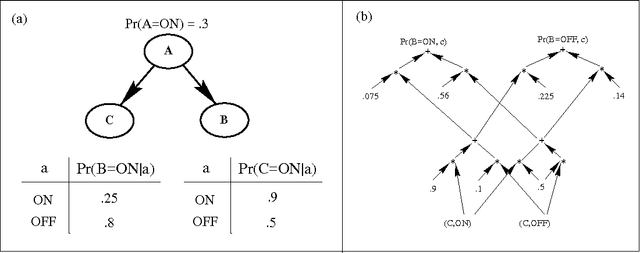
We describe a new paradigm for implementing inference in belief networks, which relies on compiling a belief network into an arithmetic expression called a Query DAG (Q-DAG). Each non-leaf node of a Q-DAG represents a numeric operation, a number, or a symbol for evidence. Each leaf node of a Q-DAG represents the answer to a network query, that is, the probability of some event of interest. It appears that Q-DAGs can be generated using any of the algorithms for exact inference in belief networks --- we show how they can be generated using clustering and conditioning algorithms. The time and space complexity of a Q-DAG generation algorithm is no worse than the time complexity of the inference algorithm on which it is based; that of a Q-DAG on-line evaluation algorithm is linear in the size of the Q-DAG, and such inference amounts to a standard evaluation of the arithmetic expression it represents. The main value of Q-DAGs is in reducing the software and hardware resources required to utilize belief networks in on-line, real-world applications. The proposed framework also facilitates the development of on-line inference on different software and hardware platforms, given the simplicity of the Q-DAG evaluation algorithm. This paper describes this new paradigm for probabilistic inference, explaining how it works, its uses, and outlines some of the research directions that it leads to.

A Logical Interpretation of Dempster-Shafer Theory, with Application to Visual Recognition

We formulate Dempster Shafer Belief functions in terms of Propositional Logic using the implicit notion of provability underlying Dempster Shafer Theory. Given a set of propositional clauses, assigning weights to certain propositional literals enables the Belief functions to be explicitly computed using Network Reliability techniques. Also, the logical procedure corresponding to updating Belief functions using Dempster's Rule of Combination is shown. This analysis formalizes the implementation of Belief functions within an Assumption-based Truth Maintenance System (ATMS). We describe the extension of an ATMS-based visual recognition system, VICTORS, with this logical formulation of Dempster Shafer theory. Without Dempster Shafer theory, VICTORS computes all possible visual interpretations (i.e. all logical models) without determining the best interpretation(s). Incorporating Dempster Shafer theory enables optimal visual interpretations to be computed and a logical semantics to be maintained.

What is an Optimal Diagnosis?

Within diagnostic reasoning there have been a number of proposed definitions of a diagnosis, and thus of the most likely diagnosis, including most probable posterior hypothesis, most probable interpretation, most probable covering hypothesis, etc. Most of these approaches assume that the most likely diagnosis must be computed, and that a definition of what should be computed can be made a priori, independent of what the diagnosis is used for. We argue that the diagnostic problem, as currently posed, is incomplete: it does not consider how the diagnosis is to be used, or the utility associated with the treatment of the abnormalities. In this paper we analyze several well-known definitions of diagnosis, showing that the different definitions of the most likely diagnosis have different qualitative meanings, even given the same input data. We argue that the most appropriate definition of (optimal) diagnosis needs to take into account the utility of outcomes and what the diagnosis is used for.

Dynamic Network Updating Techniques For Diagnostic Reasoning

A new probabilistic network construction system, DYNASTY, is proposed for diagnostic reasoning given variables whose probabilities change over time. Diagnostic reasoning is formulated as a sequential stochastic process, and is modeled using influence diagrams. Given a set O of observations, DYNASTY creates an influence diagram in order to devise the best action given O. Sensitivity analyses are conducted to determine if the best network has been created, given the uncertainty in network parameters and topology. DYNASTY uses an equivalence class approach to provide decision thresholds for the sensitivity analysis. This equivalence-class approach to diagnostic reasoning differentiates diagnoses only if the required actions are different. A set of network-topology updating algorithms are proposed for dynamically updating the network when necessary.

Tradeoffs in Constructing and Evaluating Temporal Influence Diagrams

This paper addresses the tradeoffs which need to be considered in reasoning using probabilistic network representations, such as Influence Diagrams (IDs). In particular, we examine the tradeoffs entailed in using Temporal Influence Diagrams (TIDs) which adequately capture the temporal evolution of a dynamic system without prohibitive data and computational requirements. Three approaches for TID construction which make different tradeoffs are examined: (1) tailoring the network at each time interval to the data available (rather then just copying the original Bayes Network for all time intervals); (2) modeling the evolution of a parsimonious subset of variables (rather than all variables); and (3) model selection approaches, which seek to minimize some measure of the predictive accuracy of the model without introducing too many parameters, which might cause "overfitting" of the model. Methods of evaluating the accuracy/efficiency of the tradeoffs are proposed.

Knowledge Engineering for Large Belief Networks

We present several techniques for knowledge engineering of large belief networks (BNs) based on the our experiences with a network derived from a large medical knowledge base. The noisyMAX, a generalization of the noisy-OR gate, is used to model causal in dependence in a BN with multi-valued variables. We describe the use of leak probabilities to enforce the closed-world assumption in our model. We present Netview, a visualization tool based on causal independence and the use of leak probabilities. The Netview software allows knowledge engineers to dynamically view sub-networks for knowledge engineering, and it provides version control for editing a BN. Netview generates sub-networks in which leak probabilities are dynamically updated to reflect the missing portions of the network.

An Experimental Comparison of Numerical and Qualitative Probabilistic Reasoning

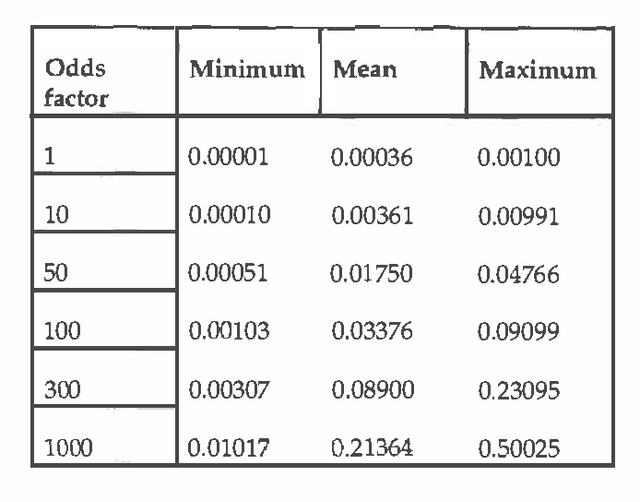
Qualitative and infinitesimal probability schemes are consistent with the axioms of probability theory, but avoid the need for precise numerical probabilities. Using qualitative probabilities could substantially reduce the effort for knowledge engineering and improve the robustness of results. We examine experimentally how well infinitesimal probabilities (the kappa-calculus of Goldszmidt and Pearl) perform a diagnostic task - troubleshooting a car that will not start by comparison with a conventional numerical belief network. We found the infinitesimal scheme to be as good as the numerical scheme in identifying the true fault. The performance of the infinitesimal scheme worsens significantly for prior fault probabilities greater than 0.03. These results suggest that infinitesimal probability methods may be of substantial practical value for machine diagnosis with small prior fault probabilities.

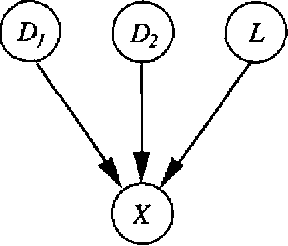
Abstraction in Belief Networks: The Role of Intermediate States in Diagnostic Reasoning

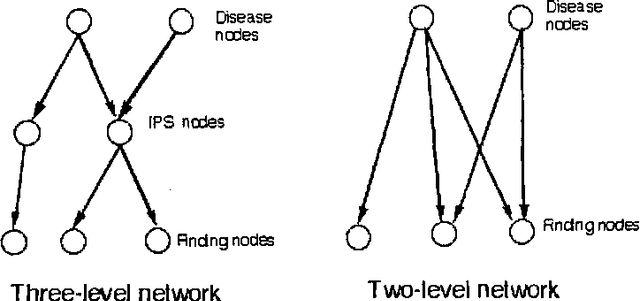
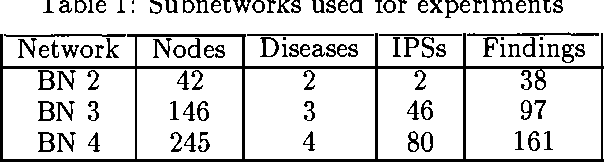
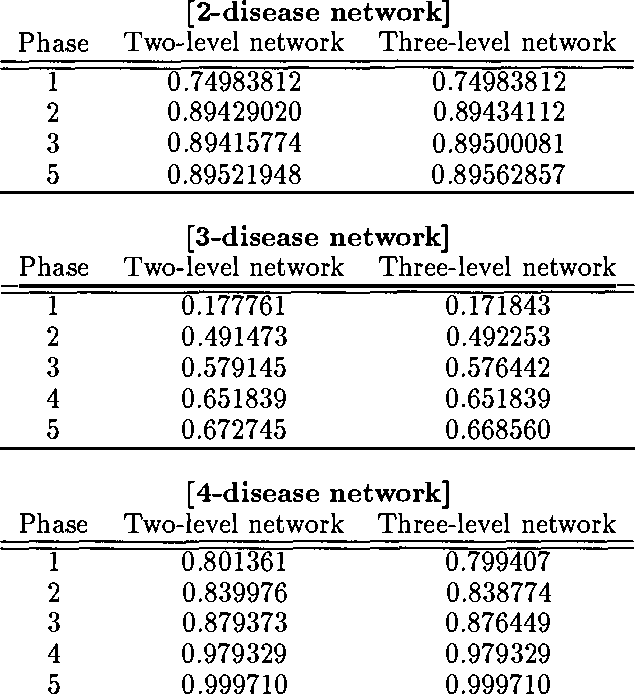
Bayesian belief networks are bing increasingly used as a knowledge representation for diagnostic reasoning. One simple method for conducting diagnostic reasoning is to represent system faults and observations only. In this paper, we investigate how having intermediate nodes-nodes other than fault and observation nodes affects the diagnostic performance of a Bayesian belief network. We conducted a series of experiments on a set of real belief networks for medical diagnosis in liver and bile disease. We compared the effects on diagnostic performance of a two-level network consisting just of disease and finding nodes with that of a network which models intermediate pathophysiological disease states as well. We provide some theoretical evidence for differences observed between the abstracted two-level network and the full network.

Why Is Diagnosis Using Belief Networks Insensitive to Imprecision In Probabilities?

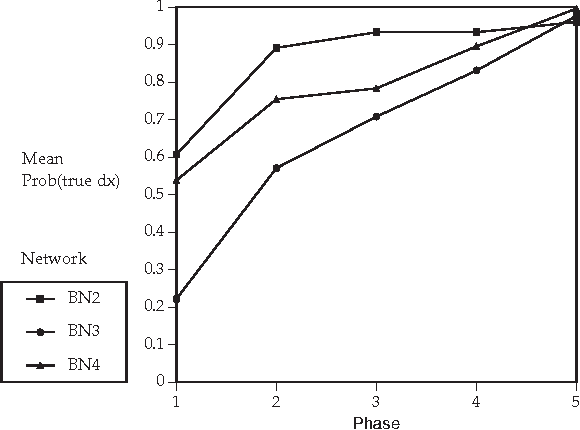
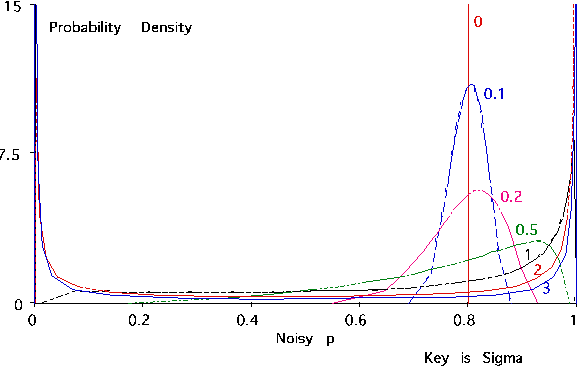
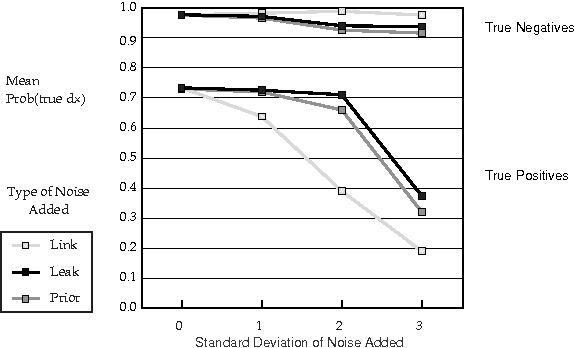
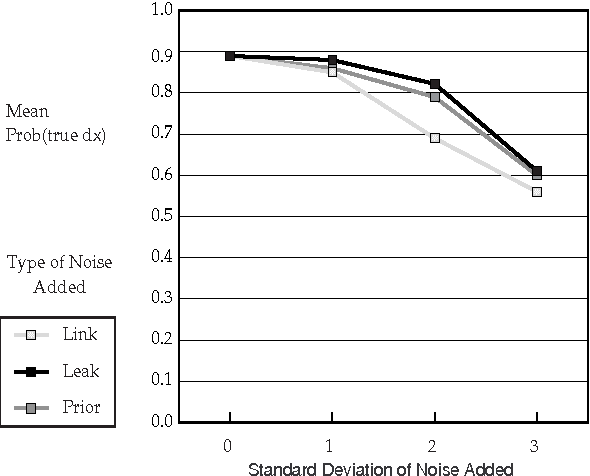
Recent research has found that diagnostic performance with Bayesian belief networks is often surprisingly insensitive to imprecision in the numerical probabilities. For example, the authors have recently completed an extensive study in which they applied random noise to the numerical probabilities in a set of belief networks for medical diagnosis, subsets of the CPCS network, a subset of the QMR (Quick Medical Reference) focused on liver and bile diseases. The diagnostic performance in terms of the average probabilities assigned to the actual diseases showed small sensitivity even to large amounts of noise. In this paper, we summarize the findings of this study and discuss possible explanations of this low sensitivity. One reason is that the criterion for performance is average probability of the true hypotheses, rather than average error in probability, which is insensitive to symmetric noise distributions. But, we show that even asymmetric, logodds-normal noise has modest effects. A second reason is that the gold-standard posterior probabilities are often near zero or one, and are little disturbed by noise.

A Standard Approach for Optimizing Belief Network Inference using Query DAGs

This paper proposes a novel, algorithm-independent approach to optimizing belief network inference. rather than designing optimizations on an algorithm by algorithm basis, we argue that one should use an unoptimized algorithm to generate a Q-DAG, a compiled graphical representation of the belief network, and then optimize the Q-DAG and its evaluator instead. We present a set of Q-DAG optimizations that supplant optimizations designed for traditional inference algorithms, including zero compression, network pruning and caching. We show that our Q-DAG optimizations require time linear in the Q-DAG size, and significantly simplify the process of designing algorithms for optimizing belief network inference.