Query DAGs: A Practical Paradigm for Implementing Belief Network Inference
Paper and Code
Aug 07, 2014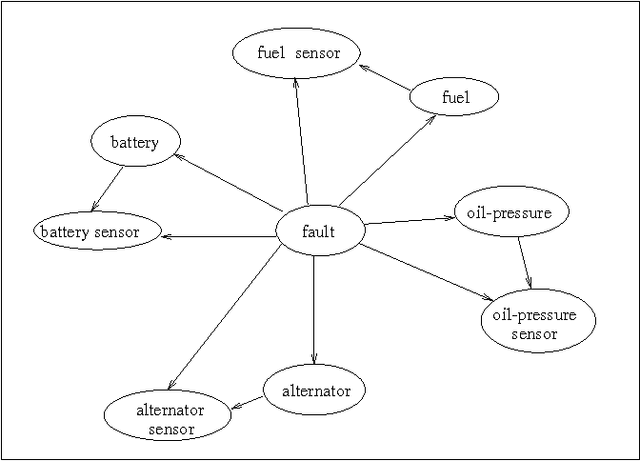
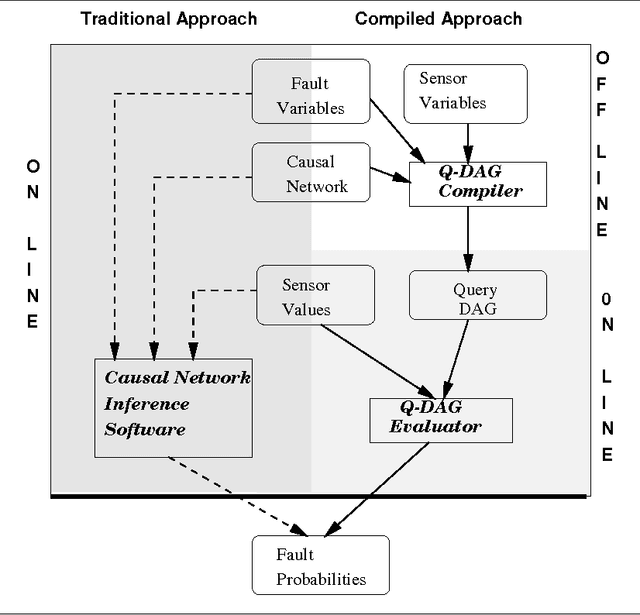
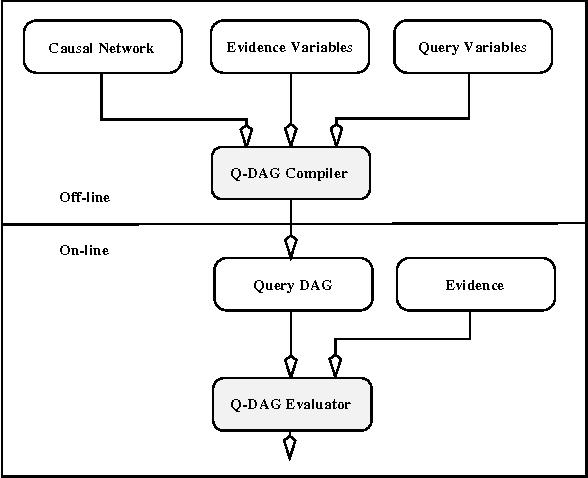
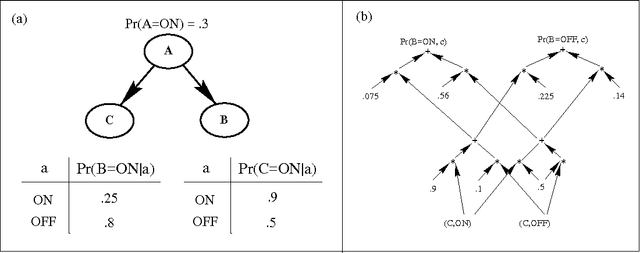
We describe a new paradigm for implementing inference in belief networks, which relies on compiling a belief network into an arithmetic expression called a Query DAG (Q-DAG). Each non-leaf node of a Q-DAG represents a numeric operation, a number, or a symbol for evidence. Each leaf node of a Q-DAG represents the answer to a network query, that is, the probability of some event of interest. It appears that Q-DAGs can be generated using any of the algorithms for exact inference in belief networks --- we show how they can be generated using clustering and conditioning algorithms. The time and space complexity of a Q-DAG generation algorithm is no worse than the time complexity of the inference algorithm on which it is based; that of a Q-DAG on-line evaluation algorithm is linear in the size of the Q-DAG, and such inference amounts to a standard evaluation of the arithmetic expression it represents. The main value of Q-DAGs is in reducing the software and hardware resources required to utilize belief networks in on-line, real-world applications. The proposed framework also facilitates the development of on-line inference on different software and hardware platforms, given the simplicity of the Q-DAG evaluation algorithm. This paper describes this new paradigm for probabilistic inference, explaining how it works, its uses, and outlines some of the research directions that it leads to.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge