Efficient Search-Based Inference for Noisy-OR Belief Networks: TopEpsilon

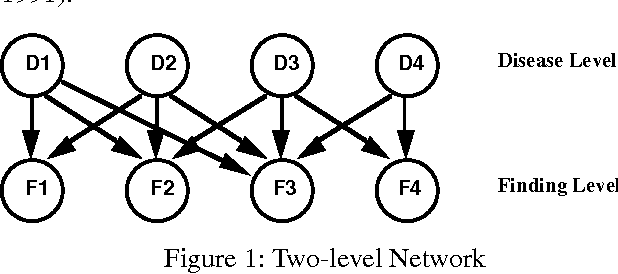
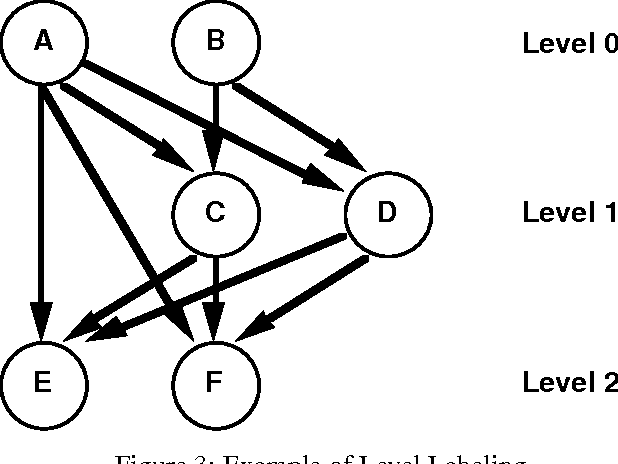
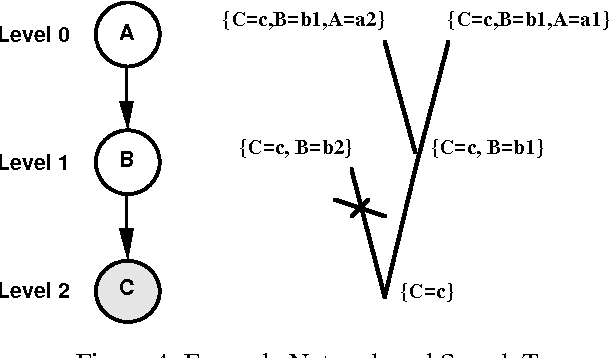
Inference algorithms for arbitrary belief networks are impractical for large, complex belief networks. Inference algorithms for specialized classes of belief networks have been shown to be more efficient. In this paper, we present a search-based algorithm for approximate inference on arbitrary, noisy-OR belief networks, generalizing earlier work on search-based inference for two-level, noisy-OR belief networks. Initial experimental results appear promising.

Why Is Diagnosis Using Belief Networks Insensitive to Imprecision In Probabilities?

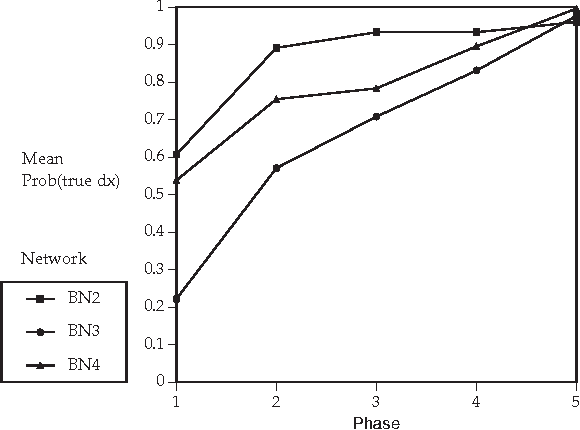
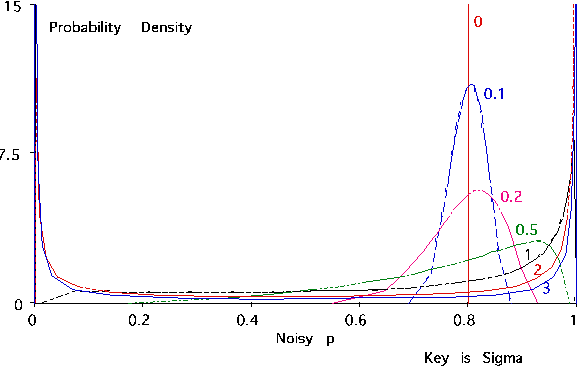
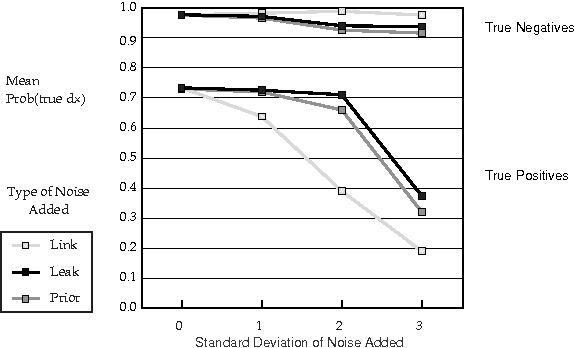
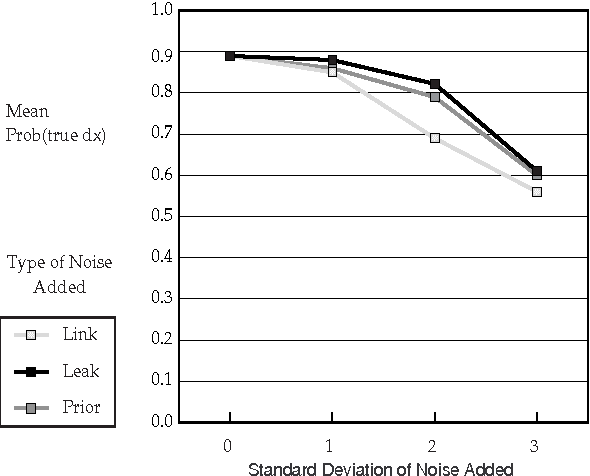
Recent research has found that diagnostic performance with Bayesian belief networks is often surprisingly insensitive to imprecision in the numerical probabilities. For example, the authors have recently completed an extensive study in which they applied random noise to the numerical probabilities in a set of belief networks for medical diagnosis, subsets of the CPCS network, a subset of the QMR (Quick Medical Reference) focused on liver and bile diseases. The diagnostic performance in terms of the average probabilities assigned to the actual diseases showed small sensitivity even to large amounts of noise. In this paper, we summarize the findings of this study and discuss possible explanations of this low sensitivity. One reason is that the criterion for performance is average probability of the true hypotheses, rather than average error in probability, which is insensitive to symmetric noise distributions. But, we show that even asymmetric, logodds-normal noise has modest effects. A second reason is that the gold-standard posterior probabilities are often near zero or one, and are little disturbed by noise.