An Experimental Comparison of Numerical and Qualitative Probabilistic Reasoning

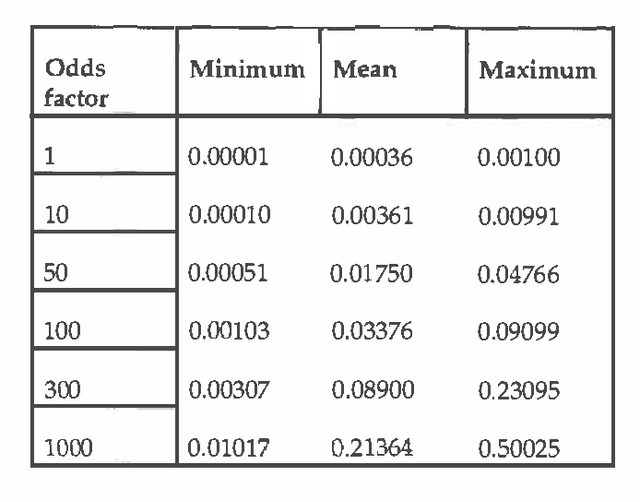
Qualitative and infinitesimal probability schemes are consistent with the axioms of probability theory, but avoid the need for precise numerical probabilities. Using qualitative probabilities could substantially reduce the effort for knowledge engineering and improve the robustness of results. We examine experimentally how well infinitesimal probabilities (the kappa-calculus of Goldszmidt and Pearl) perform a diagnostic task - troubleshooting a car that will not start by comparison with a conventional numerical belief network. We found the infinitesimal scheme to be as good as the numerical scheme in identifying the true fault. The performance of the infinitesimal scheme worsens significantly for prior fault probabilities greater than 0.03. These results suggest that infinitesimal probability methods may be of substantial practical value for machine diagnosis with small prior fault probabilities.

Backward Simulation in Bayesian Networks

Backward simulation is an approximate inference technique for Bayesian belief networks. It differs from existing simulation methods in that it starts simulation from the known evidence and works backward (i.e., contrary to the direction of the arcs). The technique's focus on the evidence leads to improved convergence in situations where the posterior beliefs are dominated by the evidence rather than by the prior probabilities. Since this class of situations is large, the technique may make practical the application of approximate inference in Bayesian belief networks to many real-world problems.

Why Is Diagnosis Using Belief Networks Insensitive to Imprecision In Probabilities?

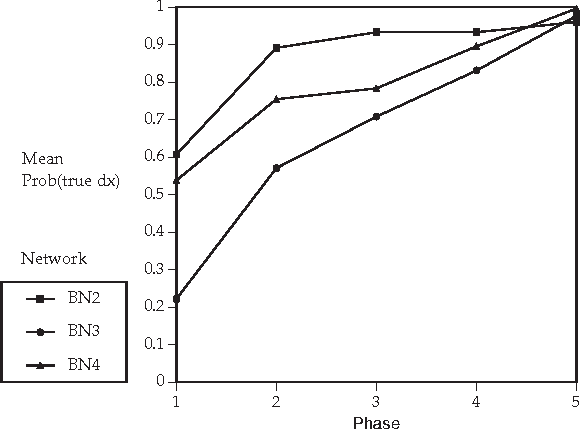
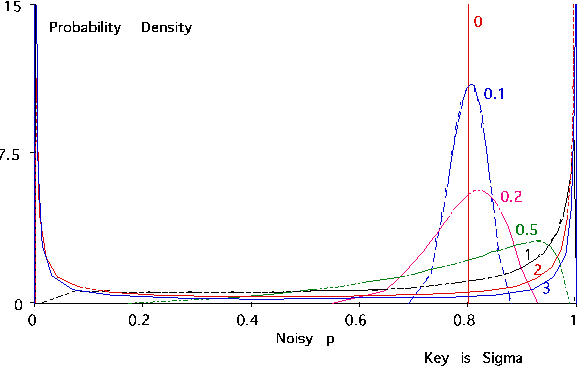
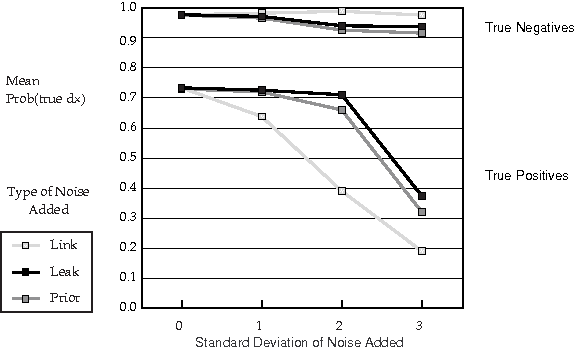
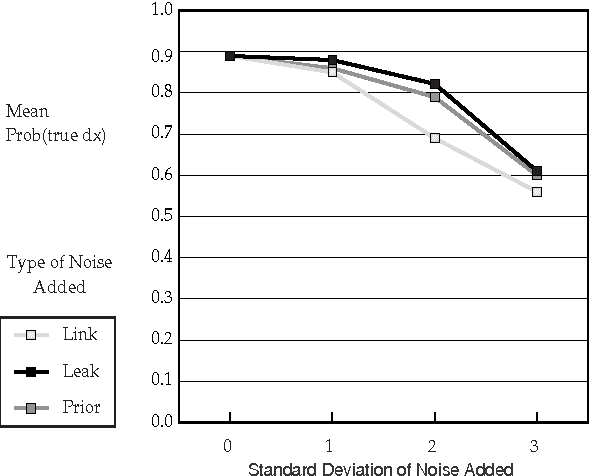
Recent research has found that diagnostic performance with Bayesian belief networks is often surprisingly insensitive to imprecision in the numerical probabilities. For example, the authors have recently completed an extensive study in which they applied random noise to the numerical probabilities in a set of belief networks for medical diagnosis, subsets of the CPCS network, a subset of the QMR (Quick Medical Reference) focused on liver and bile diseases. The diagnostic performance in terms of the average probabilities assigned to the actual diseases showed small sensitivity even to large amounts of noise. In this paper, we summarize the findings of this study and discuss possible explanations of this low sensitivity. One reason is that the criterion for performance is average probability of the true hypotheses, rather than average error in probability, which is insensitive to symmetric noise distributions. But, we show that even asymmetric, logodds-normal noise has modest effects. A second reason is that the gold-standard posterior probabilities are often near zero or one, and are little disturbed by noise.