Higher-Order DisCoCat (Peirce-Lambek-Montague semantics)

We propose a new definition of higher-order DisCoCat (categorical compositional distributional) models where the meaning of a word is not a diagram, but a diagram-valued higher-order function. Our models can be seen as a variant of Montague semantics based on a lambda calculus where the primitives act on string diagrams rather than logical formulae. As a special case, we show how to translate from the Lambek calculus into Peirce's system beta for first-order logic. This allows us to give a purely diagrammatic treatment of higher-order and non-linear processes in natural language semantics: adverbs, prepositions, negation and quantifiers. The theoretical definition presented in this article comes with a proof-of-concept implementation in DisCoPy, the Python library for string diagrams.

Categorical Tools for Natural Language Processing

This thesis develops the translation between category theory and computational linguistics as a foundation for natural language processing. The three chapters deal with syntax, semantics and pragmatics. First, string diagrams provide a unified model of syntactic structures in formal grammars. Second, functors compute semantics by turning diagrams into logical, tensor, neural or quantum computation. Third, the resulting functorial models can be composed to form games where equilibria are the solutions of language processing tasks. This framework is implemented as part of DisCoPy, the Python library for computing with string diagrams. We describe the correspondence between categorical, linguistic and computational structures, and demonstrate their applications in compositional natural language processing.

lambeq: An Efficient High-Level Python Library for Quantum NLP

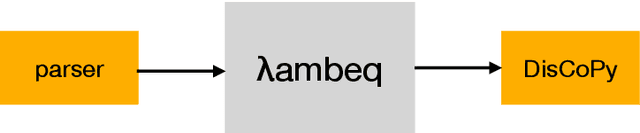
We present lambeq, the first high-level Python library for Quantum Natural Language Processing (QNLP). The open-source toolkit offers a detailed hierarchy of modules and classes implementing all stages of a pipeline for converting sentences to string diagrams, tensor networks, and quantum circuits ready to be used on a quantum computer. lambeq supports syntactic parsing, rewriting and simplification of string diagrams, ansatz creation and manipulation, as well as a number of compositional models for preparing quantum-friendly representations of sentences, employing various degrees of syntax sensitivity. We present the generic architecture and describe the most important modules in detail, demonstrating the usage with illustrative examples. Further, we test the toolkit in practice by using it to perform a number of experiments on simple NLP tasks, implementing both classical and quantum pipelines.

How to make qubits speak

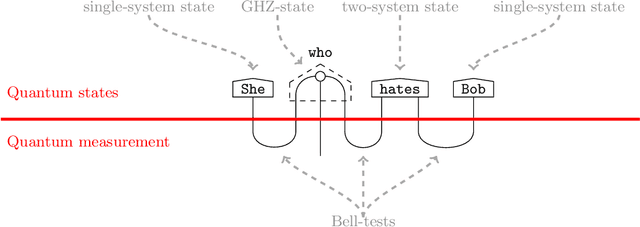
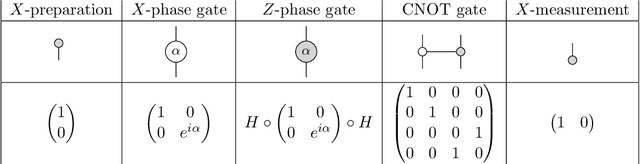
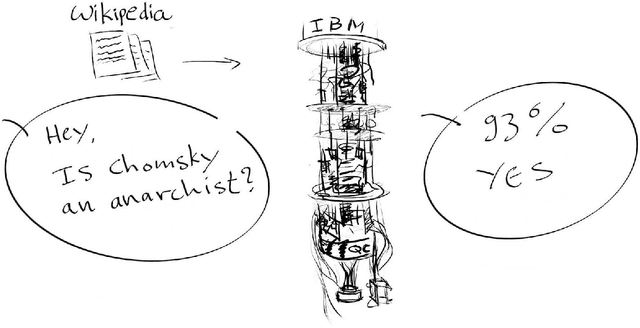
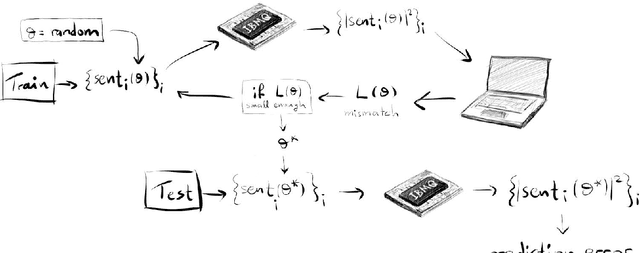
This is a story about making quantum computers speak, and doing so in a quantum-native, compositional and meaning-aware manner. Recently we did question-answering with an actual quantum computer. We explain what we did, stress that this was all done in terms of pictures, and provide many pointers to the related literature. In fact, besides natural language, many other things can be implemented in a quantum-native, compositional and meaning-aware manner, and we provide the reader with some indications of that broader pictorial landscape, including our account on the notion of compositionality. We also provide some guidance for the actual execution, so that the reader can give it a go as well.

Diagrammatic Differentiation for Quantum Machine Learning

We introduce diagrammatic differentiation for tensor calculus by generalising the dual number construction from rigs to monoidal categories. Applying this to ZX diagrams, we show how to calculate diagrammatically the gradient of a linear map with respect to a phase parameter. For diagrams of parametrised quantum circuits, we get the well-known parameter-shift rule at the basis of many variational quantum algorithms. We then extend our method to the automatic differentation of hybrid classical-quantum circuits, using diagrams with bubbles to encode arbitrary non-linear operators. Moreover, diagrammatic differentiation comes with an open-source implementation in DisCoPy, the Python library for monoidal categories. Diagrammatic gradients of classical-quantum circuits can then be simplified using the PyZX library and executed on quantum hardware via the tket compiler. This opens the door to many practical applications harnessing both the structure of string diagrams and the computational power of quantum machine learning.

Grammar-Aware Question-Answering on Quantum Computers

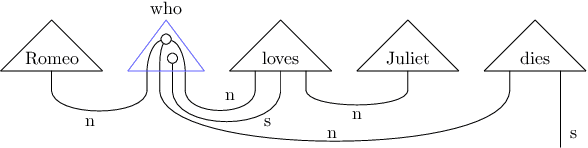
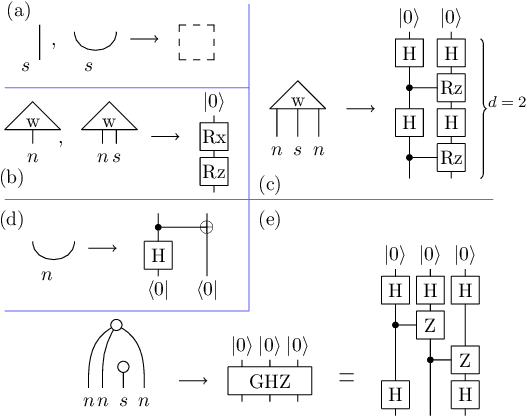
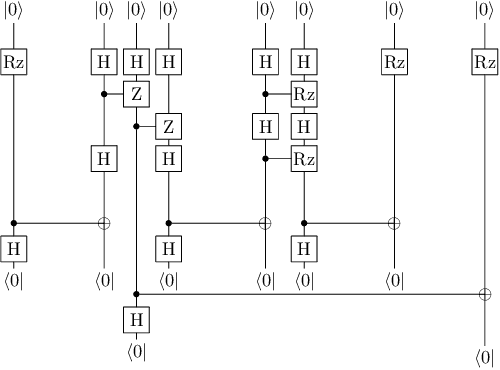
Natural language processing (NLP) is at the forefront of great advances in contemporary AI, and it is arguably one of the most challenging areas of the field. At the same time, with the steady growth of quantum hardware and notable improvements towards implementations of quantum algorithms, we are approaching an era when quantum computers perform tasks that cannot be done on classical computers with a reasonable amount of resources. This provides a new range of opportunities for AI, and for NLP specifically. Earlier work has already demonstrated a potential quantum advantage for NLP in a number of manners: (i) algorithmic speedups for search-related or classification tasks, which are the most dominant tasks within NLP, (ii) exponentially large quantum state spaces allow for accommodating complex linguistic structures, (iii) novel models of meaning employing density matrices naturally model linguistic phenomena such as hyponymy and linguistic ambiguity, among others. In this work, we perform the first implementation of an NLP task on noisy intermediate-scale quantum (NISQ) hardware. Sentences are instantiated as parameterised quantum circuits. We encode word-meanings in quantum states and we explicitly account for grammatical structure, which even in mainstream NLP is not commonplace, by faithfully hard-wiring it as entangling operations. This makes our approach to quantum natural language processing (QNLP) particularly NISQ-friendly. Our novel QNLP model shows concrete promise for scalability as the quality of the quantum hardware improves in the near future.

Foundations for Near-Term Quantum Natural Language Processing

We provide conceptual and mathematical foundations for near-term quantum natural language processing (QNLP), and do so in quantum computer scientist friendly terms. We opted for an expository presentation style, and provide references for supporting empirical evidence and formal statements concerning mathematical generality. We recall how the quantum model for natural language that we employ canonically combines linguistic meanings with rich linguistic structure, most notably grammar. In particular, the fact that it takes a quantum-like model to combine meaning and structure, establishes QNLP as quantum-native, on par with simulation of quantum systems. Moreover, the now leading Noisy Intermediate-Scale Quantum (NISQ) paradigm for encoding classical data on quantum hardware, variational quantum circuits, makes NISQ exceptionally QNLP-friendly: linguistic structure can be encoded as a free lunch, in contrast to the apparently exponentially expensive classical encoding of grammar. Quantum speed-up for QNLP tasks has already been established in previous work with Will Zeng. Here we provide a broader range of tasks which all enjoy the same advantage. Diagrammatic reasoning is at the heart of QNLP. Firstly, the quantum model interprets language as quantum processes via the diagrammatic formalism of categorical quantum mechanics. Secondly, these diagrams are via ZX-calculus translated into quantum circuits. Parameterisations of meanings then become the circuit variables to be learned. Our encoding of linguistic structure within quantum circuits also embodies a novel approach for establishing word-meanings that goes beyond the current standards in mainstream AI, by placing linguistic structure at the heart of Wittgenstein's meaning-is-context.

Functorial Language Games for Question Answering

We present some categorical investigations into Wittgenstein's language-games, with applications to game-theoretic pragmatics and question-answering in natural language processing.

Montague Semantics for Lambek Pregroups

Lambek pregroups are algebraic structures modelling natural language syntax, while Montague captures semantics as a homomorphism from syntax to first-order logic. We introduce the variant RelCoCat of the categorical compositional distributional (DisCoCat) models of Coecke et al. where linear maps are replaced by relations. Our main result is a factorisation of RelCoCat models through free cartesian bicategories, as a corollary we get a logspace reduction from the semantics problem to the evaluation of conjunctive queries. Finally, we define question answering as an NP-complete problem.

Towards Compositional Distributional Discourse Analysis

Categorical compositional distributional semantics provide a method to derive the meaning of a sentence from the meaning of its individual words: the grammatical reduction of a sentence automatically induces a linear map for composing the word vectors obtained from distributional semantics. In this paper, we extend this passage from word-to-sentence to sentence-to-discourse composition. To achieve this we introduce a notion of basic anaphoric discourses as a mid-level representation between natural language discourse formalised in terms of basic discourse representation structures (DRS); and knowledge base queries over the Semantic Web as described by basic graph patterns in the Resource Description Framework (RDF). This provides a high-level specification for compositional algorithms for question answering and anaphora resolution, and allows us to give a picture of natural language understanding as a process involving both statistical and logical resources.