Dan Marsden
University of Oxford
Towards Compositional Distributional Discourse Analysis
Nov 08, 2018Abstract:Categorical compositional distributional semantics provide a method to derive the meaning of a sentence from the meaning of its individual words: the grammatical reduction of a sentence automatically induces a linear map for composing the word vectors obtained from distributional semantics. In this paper, we extend this passage from word-to-sentence to sentence-to-discourse composition. To achieve this we introduce a notion of basic anaphoric discourses as a mid-level representation between natural language discourse formalised in terms of basic discourse representation structures (DRS); and knowledge base queries over the Semantic Web as described by basic graph patterns in the Resource Description Framework (RDF). This provides a high-level specification for compositional algorithms for question answering and anaphora resolution, and allows us to give a picture of natural language understanding as a process involving both statistical and logical resources.
* In Proceedings CAPNS 2018, arXiv:1811.02701
Internal Wiring of Cartesian Verbs and Prepositions
Nov 08, 2018
Abstract:Categorical compositional distributional semantics (CCDS) allows one to compute the meaning of phrases and sentences from the meaning of their constituent words. A type-structure carried over from the traditional categorial model of grammar a la Lambek becomes a 'wire-structure' that mediates the interaction of word meanings. However, CCDS has a much richer logical structure than plain categorical semantics in that certain words can also be given an 'internal wiring' that either provides their entire meaning or reduces the size their meaning space. Previous examples of internal wiring include relative pronouns and intersective adjectives. Here we establish the same for a large class of well-behaved transitive verbs to which we refer as Cartesian verbs, and reduce the meaning space from a ternary tensor to a unary one. Some experimental evidence is also provided.
* In Proceedings CAPNS 2018, arXiv:1811.02701
Proceedings of the 2018 Workshop on Compositional Approaches in Physics, NLP, and Social Sciences
Nov 06, 2018Abstract:The ability to compose parts to form a more complex whole, and to analyze a whole as a combination of elements, is desirable across disciplines. This workshop bring together researchers applying compositional approaches to physics, NLP, cognitive science, and game theory. Within NLP, a long-standing aim is to represent how words can combine to form phrases and sentences. Within the framework of distributional semantics, words are represented as vectors in vector spaces. The categorical model of Coecke et al. [2010], inspired by quantum protocols, has provided a convincing account of compositionality in vector space models of NLP. There is furthermore a history of vector space models in cognitive science. Theories of categorization such as those developed by Nosofsky [1986] and Smith et al. [1988] utilise notions of distance between feature vectors. More recently G\"ardenfors [2004, 2014] has developed a model of concepts in which conceptual spaces provide geometric structures, and information is represented by points, vectors and regions in vector spaces. The same compositional approach has been applied to this formalism, giving conceptual spaces theory a richer model of compositionality than previously [Bolt et al., 2018]. Compositional approaches have also been applied in the study of strategic games and Nash equilibria. In contrast to classical game theory, where games are studied monolithically as one global object, compositional game theory works bottom-up by building large and complex games from smaller components. Such an approach is inherently difficult since the interaction between games has to be considered. Research into categorical compositional methods for this field have recently begun [Ghani et al., 2018]. Moreover, the interaction between the three disciplines of cognitive science, linguistics and game theory is a fertile ground for research. Game theory in cognitive science is a well-established area [Camerer, 2011]. Similarly game theoretic approaches have been applied in linguistics [J\"ager, 2008]. Lastly, the study of linguistics and cognitive science is intimately intertwined [Smolensky and Legendre, 2006, Jackendoff, 2007]. Physics supplies compositional approaches via vector spaces and categorical quantum theory, allowing the interplay between the three disciplines to be examined.
Interacting Conceptual Spaces I : Grammatical Composition of Concepts
Sep 29, 2017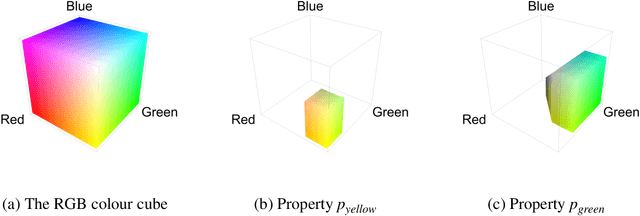

Abstract:The categorical compositional approach to meaning has been successfully applied in natural language processing, outperforming other models in mainstream empirical language processing tasks. We show how this approach can be generalized to conceptual space models of cognition. In order to do this, first we introduce the category of convex relations as a new setting for categorical compositional semantics, emphasizing the convex structure important to conceptual space applications. We then show how to construct conceptual spaces for various types such as nouns, adjectives and verbs. Finally we show by means of examples how concepts can be systematically combined to establish the meanings of composite phrases from the meanings of their constituent parts. This provides the mathematical underpinnings of a new compositional approach to cognition.
Ambiguity and Incomplete Information in Categorical Models of Language
Jan 03, 2017Abstract:We investigate notions of ambiguity and partial information in categorical distributional models of natural language. Probabilistic ambiguity has previously been studied using Selinger's CPM construction. This construction works well for models built upon vector spaces, as has been shown in quantum computational applications. Unfortunately, it doesn't seem to provide a satisfactory method for introducing mixing in other compact closed categories such as the category of sets and binary relations. We therefore lack a uniform strategy for extending a category to model imprecise linguistic information. In this work we adopt a different approach. We analyze different forms of ambiguous and incomplete information, both with and without quantitative probabilistic data. Each scheme then corresponds to a suitable enrichment of the category in which we model language. We view different monads as encapsulating the informational behaviour of interest, by analogy with their use in modelling side effects in computation. Previous results of Jacobs then allow us to systematically construct suitable bases for enrichment. We show that we can freely enrich arbitrary dagger compact closed categories in order to capture all the phenomena of interest, whilst retaining the important dagger compact closed structure. This allows us to construct a model with real convex combination of binary relations that makes non-trivial use of the scalars. Finally we relate our various different enrichments, showing that finite subconvex algebra enrichment covers all the effects under consideration.
* In Proceedings QPL 2016, arXiv:1701.00242
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge