Reinforcement Learning in Categorical Cybernetics

We show that several major algorithms of reinforcement learning (RL) fit into the framework of categorical cybernetics, that is to say, parametrised bidirectional processes. We build on our previous work in which we show that value iteration can be represented by precomposition with a certain optic. The outline of the main construction in this paper is: (1) We extend the Bellman operators to parametrised optics that apply to action-value functions and depend on a sample. (2) We apply a representable contravariant functor, obtaining a parametrised function that applies the Bellman iteration. (3) This parametrised function becomes the backward pass of another parametrised optic that represents the model, which interacts with an environment via an agent. Thus, parametrised optics appear in two different ways in our construction, with one becoming part of the other. As we show, many of the major classes of algorithms in RL can be seen as different extremal cases of this general setup: dynamic programming, Monte Carlo methods, temporal difference learning, and deep RL. We see this as strong evidence that this approach is a natural one and believe that it will be a fruitful way to think about RL in the future.

The Compositional Structure of Bayesian Inference

Bayes' rule tells us how to invert a causal process in order to update our beliefs in light of new evidence. If the process is believed to have a complex compositional structure, we may observe that the inversion of the whole can be computed piecewise in terms of the component processes. We study the structure of this compositional rule, noting that it relates to the lens pattern in functional programming. Working in a suitably general axiomatic presentation of a category of Markov kernels, we see how we can think of Bayesian inversion as a particular instance of a state-dependent morphism in a fibred category. We discuss the compositional nature of this, formulated as a functor on the underlying category and explore how this can used for a more type-driven approach to statistical inference.

From open learners to open games

The categories of open learners (due to Fong, Spivak and Tuy\'eras) and open games (due to the present author, Ghani, Winschel and Zahn) bear a very striking and unexpected similarity. The purpose of this short note is to prove that there is a faithful symmetric monoidal functor from the former to the latter, which means that any supervised neural network (without feedback or other complicating features) can be seen as an open game in a canonical way. Roughly, each parameter is controlled by a different player, and the game's best response relation encodes the dynamics of gradient descent. We suggest paths for further work exploiting the link.

Proceedings of the 2018 Workshop on Compositional Approaches in Physics, NLP, and Social Sciences

The ability to compose parts to form a more complex whole, and to analyze a whole as a combination of elements, is desirable across disciplines. This workshop bring together researchers applying compositional approaches to physics, NLP, cognitive science, and game theory. Within NLP, a long-standing aim is to represent how words can combine to form phrases and sentences. Within the framework of distributional semantics, words are represented as vectors in vector spaces. The categorical model of Coecke et al. [2010], inspired by quantum protocols, has provided a convincing account of compositionality in vector space models of NLP. There is furthermore a history of vector space models in cognitive science. Theories of categorization such as those developed by Nosofsky [1986] and Smith et al. [1988] utilise notions of distance between feature vectors. More recently G\"ardenfors [2004, 2014] has developed a model of concepts in which conceptual spaces provide geometric structures, and information is represented by points, vectors and regions in vector spaces. The same compositional approach has been applied to this formalism, giving conceptual spaces theory a richer model of compositionality than previously [Bolt et al., 2018]. Compositional approaches have also been applied in the study of strategic games and Nash equilibria. In contrast to classical game theory, where games are studied monolithically as one global object, compositional game theory works bottom-up by building large and complex games from smaller components. Such an approach is inherently difficult since the interaction between games has to be considered. Research into categorical compositional methods for this field have recently begun [Ghani et al., 2018]. Moreover, the interaction between the three disciplines of cognitive science, linguistics and game theory is a fertile ground for research. Game theory in cognitive science is a well-established area [Camerer, 2011]. Similarly game theoretic approaches have been applied in linguistics [J\"ager, 2008]. Lastly, the study of linguistics and cognitive science is intimately intertwined [Smolensky and Legendre, 2006, Jackendoff, 2007]. Physics supplies compositional approaches via vector spaces and categorical quantum theory, allowing the interplay between the three disciplines to be examined.

Towards functorial language-games

In categorical compositional semantics of natural language one studies functors from a category of grammatical derivations (such as a Lambek pregroup) to a semantic category (such as real vector spaces). We compositionally build game-theoretic semantics of sentences by taking the semantic category to be the category whose morphisms are open games. This requires some modifications to the grammar category to compensate for the failure of open games to form a compact closed category. We illustrate the theory using simple examples of Wittgenstein's language-games.

A Generalised Quantifier Theory of Natural Language in Categorical Compositional Distributional Semantics with Bialgebras

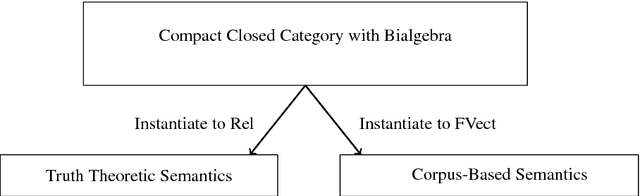
Categorical compositional distributional semantics is a model of natural language; it combines the statistical vector space models of words with the compositional models of grammar. We formalise in this model the generalised quantifier theory of natural language, due to Barwise and Cooper. The underlying setting is a compact closed category with bialgebras. We start from a generative grammar formalisation and develop an abstract categorical compositional semantics for it, then instantiate the abstract setting to sets and relations and to finite dimensional vector spaces and linear maps. We prove the equivalence of the relational instantiation to the truth theoretic semantics of generalised quantifiers. The vector space instantiation formalises the statistical usages of words and enables us to, for the first time, reason about quantified phrases and sentences compositionally in distributional semantics.