A Generalised Quantifier Theory of Natural Language in Categorical Compositional Distributional Semantics with Bialgebras
Paper and Code
Sep 02, 2017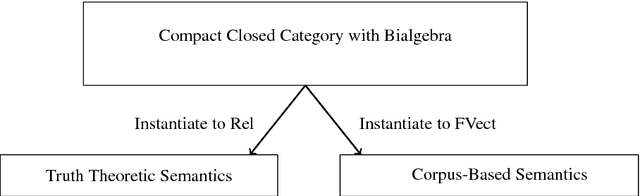
Categorical compositional distributional semantics is a model of natural language; it combines the statistical vector space models of words with the compositional models of grammar. We formalise in this model the generalised quantifier theory of natural language, due to Barwise and Cooper. The underlying setting is a compact closed category with bialgebras. We start from a generative grammar formalisation and develop an abstract categorical compositional semantics for it, then instantiate the abstract setting to sets and relations and to finite dimensional vector spaces and linear maps. We prove the equivalence of the relational instantiation to the truth theoretic semantics of generalised quantifiers. The vector space instantiation formalises the statistical usages of words and enables us to, for the first time, reason about quantified phrases and sentences compositionally in distributional semantics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge