Giorgia Minello
Graph Generation via Spectral Diffusion
Feb 29, 2024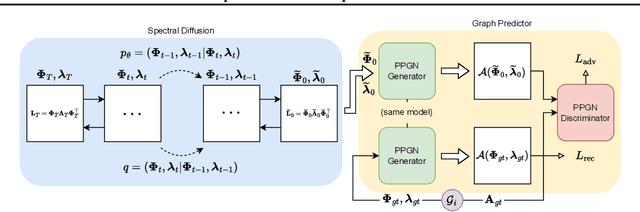
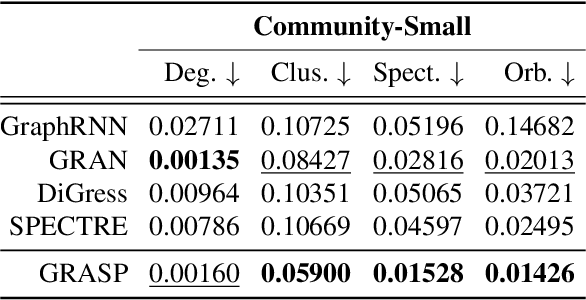
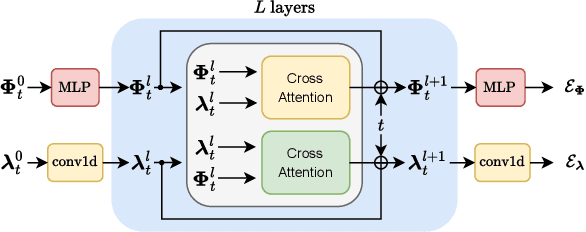
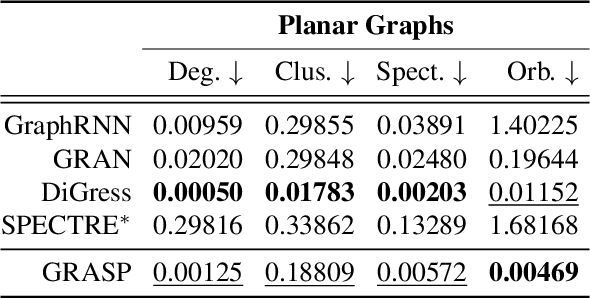
Abstract:In this paper, we present GRASP, a novel graph generative model based on 1) the spectral decomposition of the graph Laplacian matrix and 2) a diffusion process. Specifically, we propose to use a denoising model to sample eigenvectors and eigenvalues from which we can reconstruct the graph Laplacian and adjacency matrix. Our permutation invariant model can also handle node features by concatenating them to the eigenvectors of each node. Using the Laplacian spectrum allows us to naturally capture the structural characteristics of the graph and work directly in the node space while avoiding the quadratic complexity bottleneck that limits the applicability of other methods. This is achieved by truncating the spectrum, which as we show in our experiments results in a faster yet accurate generative process. An extensive set of experiments on both synthetic and real world graphs demonstrates the strengths of our model against state-of-the-art alternatives.
GNN-LoFI: a Novel Graph Neural Network through Localized Feature-based Histogram Intersection
Jan 17, 2024Abstract:Graph neural networks are increasingly becoming the framework of choice for graph-based machine learning. In this paper, we propose a new graph neural network architecture that substitutes classical message passing with an analysis of the local distribution of node features. To this end, we extract the distribution of features in the egonet for each local neighbourhood and compare them against a set of learned label distributions by taking the histogram intersection kernel. The similarity information is then propagated to other nodes in the network, effectively creating a message passing-like mechanism where the message is determined by the ensemble of the features. We perform an ablation study to evaluate the network's performance under different choices of its hyper-parameters. Finally, we test our model on standard graph classification and regression benchmarks, and we find that it outperforms widely used alternative approaches, including both graph kernels and graph neural networks.
Graph Kernel Neural Networks
Dec 14, 2021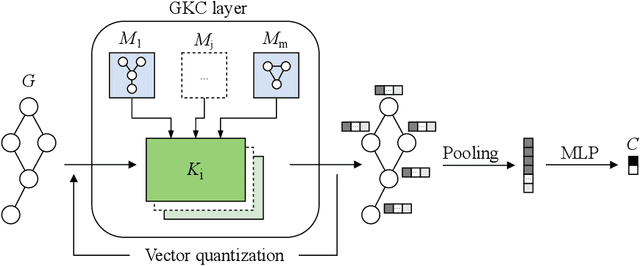
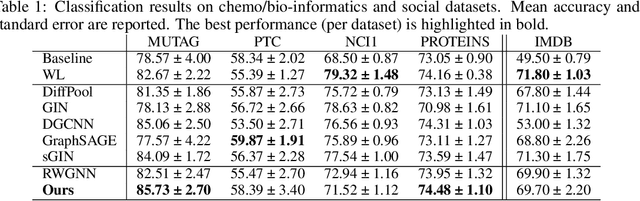

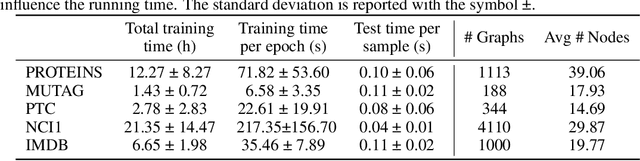
Abstract:The convolution operator at the core of many modern neural architectures can effectively be seen as performing a dot product between an input matrix and a filter. While this is readily applicable to data such as images, which can be represented as regular grids in the Euclidean space, extending the convolution operator to work on graphs proves more challenging, due to their irregular structure. In this paper, we propose to use graph kernels, i.e., kernel functions that compute an inner product on graphs, to extend the standard convolution operator to the graph domain. This allows us to define an entirely structural model that does not require computing the embedding of the input graph. Our architecture allows to plug-in any type and number of graph kernels and has the added benefit of providing some interpretability in terms of the structural masks that are learned during the training process, similarly to what happens for convolutional masks in traditional convolutional neural networks. We perform an extensive ablation study to investigate the impact of the model hyper-parameters and we show that our model achieves competitive performance on standard graph classification datasets.
LDA2Net: Digging under the surface of COVID-19 topics in scientific literature
Dec 03, 2021



Abstract:During the COVID-19 pandemic, the scientific literature related to SARS-COV-2 has been growing dramatically, both in terms of the number of publications and of its impact on people's life. This literature encompasses a varied set of sensible topics, ranging from vaccination, to protective equipment efficacy, to lockdown policy evaluation. Up to now, hundreds of thousands of papers have been uploaded on online repositories and published in scientific journals. As a result, the development of digital methods that allow an in-depth exploration of this growing literature has become a relevant issue, both to identify the topical trends of COVID-related research and to zoom-in its sub-themes. This work proposes a novel methodology, called LDA2Net, which combines topic modelling and network analysis to investigate topics under their surface. Specifically, LDA2Net exploits the frequencies of pairs of consecutive words to reconstruct the network structure of topics discussed in the Cord-19 corpus. The results suggest that the effectiveness of topic models can be magnified by enriching them with word network representations, and by using the latter to display, analyse, and explore COVID-related topics at different levels of granularity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge