Alessandro Bicciato
Graph Generation via Spectral Diffusion
Feb 29, 2024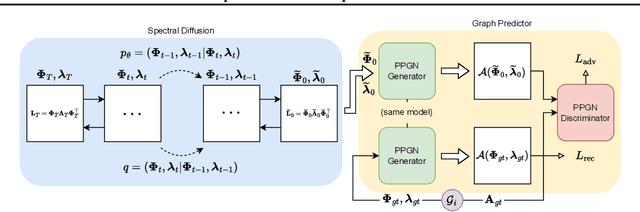
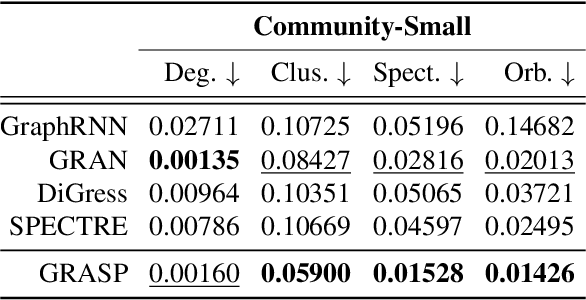
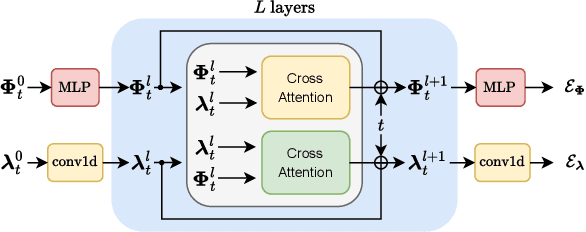
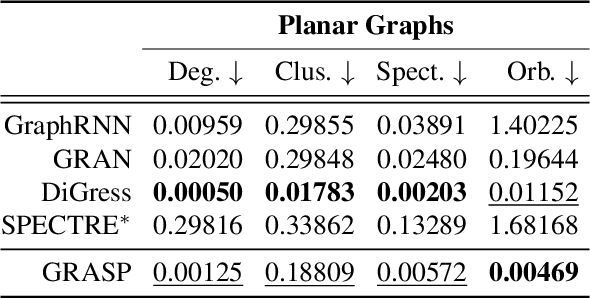
Abstract:In this paper, we present GRASP, a novel graph generative model based on 1) the spectral decomposition of the graph Laplacian matrix and 2) a diffusion process. Specifically, we propose to use a denoising model to sample eigenvectors and eigenvalues from which we can reconstruct the graph Laplacian and adjacency matrix. Our permutation invariant model can also handle node features by concatenating them to the eigenvectors of each node. Using the Laplacian spectrum allows us to naturally capture the structural characteristics of the graph and work directly in the node space while avoiding the quadratic complexity bottleneck that limits the applicability of other methods. This is achieved by truncating the spectrum, which as we show in our experiments results in a faster yet accurate generative process. An extensive set of experiments on both synthetic and real world graphs demonstrates the strengths of our model against state-of-the-art alternatives.
GNN-LoFI: a Novel Graph Neural Network through Localized Feature-based Histogram Intersection
Jan 17, 2024Abstract:Graph neural networks are increasingly becoming the framework of choice for graph-based machine learning. In this paper, we propose a new graph neural network architecture that substitutes classical message passing with an analysis of the local distribution of node features. To this end, we extract the distribution of features in the egonet for each local neighbourhood and compare them against a set of learned label distributions by taking the histogram intersection kernel. The similarity information is then propagated to other nodes in the network, effectively creating a message passing-like mechanism where the message is determined by the ensemble of the features. We perform an ablation study to evaluate the network's performance under different choices of its hyper-parameters. Finally, we test our model on standard graph classification and regression benchmarks, and we find that it outperforms widely used alternative approaches, including both graph kernels and graph neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge