Unsupervised Hierarchical Skill Discovery

We consider the problem of unsupervised skill segmentation and hierarchical structure discovery in reinforcement learning. While recent approaches have sought to segment trajectories into reusable skills or options, most rely on action labels, rewards, or handcrafted annotations, limiting their applicability. We propose a method that segments unlabelled trajectories into skills and induces a hierarchical structure over them using a grammar-based approach. The resulting hierarchy captures both low-level behaviours and their composition into higher-level skills. We evaluate our approach in high-dimensional, pixel-based environments, including Craftax and the full, unmodified version of Minecraft. Using metrics for skill segmentation, reuse, and hierarchy quality, we find that our method consistently produces more structured and semantically meaningful hierarchies than existing baselines. Furthermore, as a proof of concept for utility, we demonstrate that these discovered hierarchies accelerate and stabilise learning on downstream reinforcement learning tasks.

Beyond Sliding Windows: Learning to Manage Memory in Non-Markovian Environments

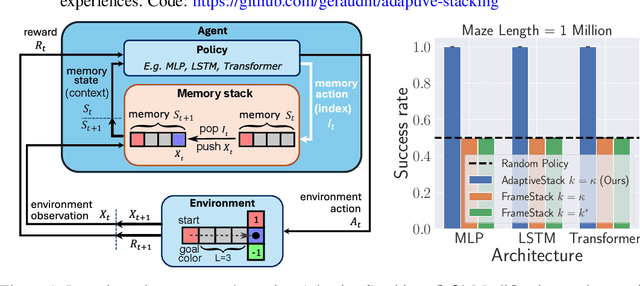
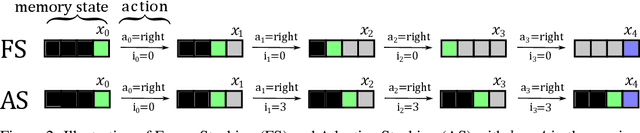
Recent success in developing increasingly general purpose agents based on sequence models has led to increased focus on the problem of deploying computationally limited agents within the vastly more complex real-world. A key challenge experienced in these more realistic domains is highly non-Markovian dependencies with respect to the agent's observations, which are less common in small controlled domains. The predominant approach for dealing with this in the literature is to stack together a window of the most recent observations (Frame Stacking), but this window size must grow with the degree of non-Markovian dependencies, which results in prohibitive computational and memory requirements for both action inference and learning. In this paper, we are motivated by the insight that in many environments that are highly non-Markovian with respect to time, the environment only causally depends on a relatively small number of observations over that time-scale. A natural direction would then be to consider meta-algorithms that maintain relatively small adaptive stacks of memories such that it is possible to express highly non-Markovian dependencies with respect to time while considering fewer observations at each step and thus experience substantial savings in both compute and memory requirements. Hence, we propose a meta-algorithm (Adaptive Stacking) for achieving exactly that with convergence guarantees and quantify the reduced computation and memory constraints for MLP, LSTM, and Transformer-based agents. Our experiments utilize popular memory tasks, which give us control over the degree of non-Markovian dependencies. This allows us to demonstrate that an appropriate meta-algorithm can learn the removal of memories not predictive of future rewards without excessive removal of important experiences. Code: https://github.com/geraudnt/adaptive-stacking

Counting Reward Automata: Sample Efficient Reinforcement Learning Through the Exploitation of Reward Function Structure

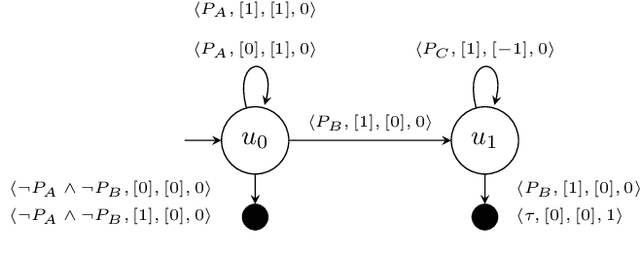
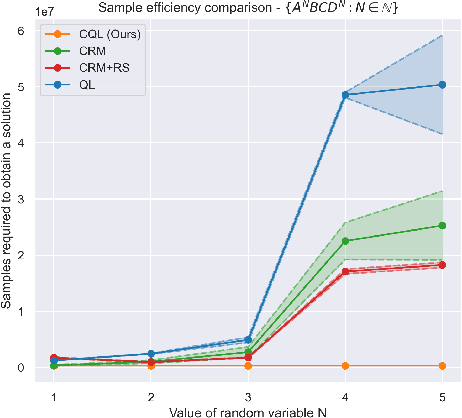
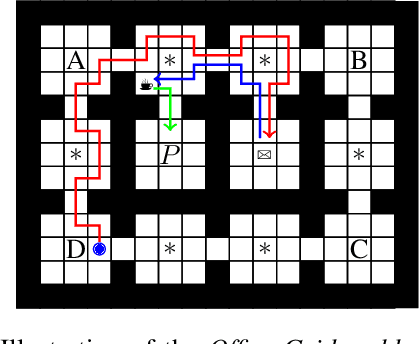
We present counting reward automata-a finite state machine variant capable of modelling any reward function expressible as a formal language. Unlike previous approaches, which are limited to the expression of tasks as regular languages, our framework allows for tasks described by unrestricted grammars. We prove that an agent equipped with such an abstract machine is able to solve a larger set of tasks than those utilising current approaches. We show that this increase in expressive power does not come at the cost of increased automaton complexity. A selection of learning algorithms are presented which exploit automaton structure to improve sample efficiency. We show that the state machines required in our formulation can be specified from natural language task descriptions using large language models. Empirical results demonstrate that our method outperforms competing approaches in terms of sample efficiency, automaton complexity, and task completion.

ROSARL: Reward-Only Safe Reinforcement Learning

An important problem in reinforcement learning is designing agents that learn to solve tasks safely in an environment. A common solution is for a human expert to define either a penalty in the reward function or a cost to be minimised when reaching unsafe states. However, this is non-trivial, since too small a penalty may lead to agents that reach unsafe states, while too large a penalty increases the time to convergence. Additionally, the difficulty in designing reward or cost functions can increase with the complexity of the problem. Hence, for a given environment with a given set of unsafe states, we are interested in finding the upper bound of rewards at unsafe states whose optimal policies minimise the probability of reaching those unsafe states, irrespective of task rewards. We refer to this exact upper bound as the "Minmax penalty", and show that it can be obtained by taking into account both the controllability and diameter of an environment. We provide a simple practical model-free algorithm for an agent to learn this Minmax penalty while learning the task policy, and demonstrate that using it leads to agents that learn safe policies in high-dimensional continuous control environments.

World Value Functions: Knowledge Representation for Learning and Planning

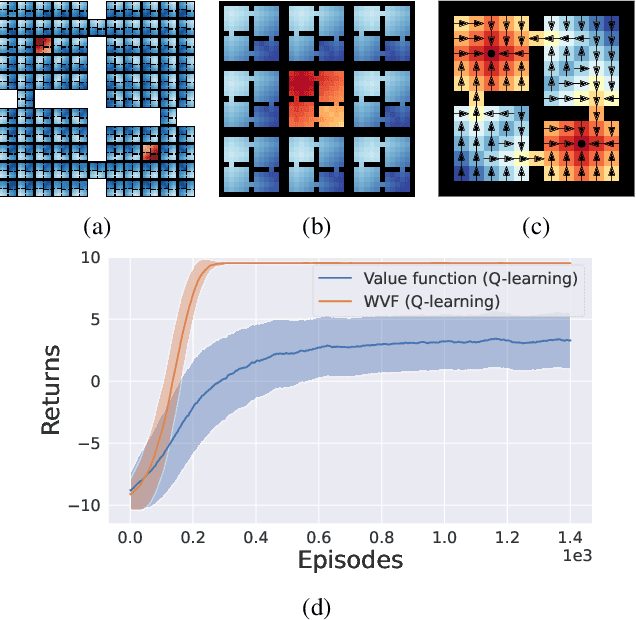
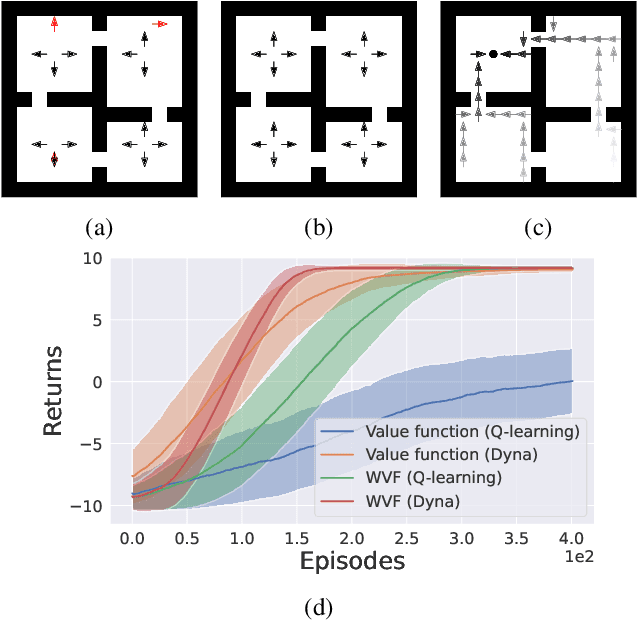
We propose world value functions (WVFs), a type of goal-oriented general value function that represents how to solve not just a given task, but any other goal-reaching task in an agent's environment. This is achieved by equipping an agent with an internal goal space defined as all the world states where it experiences a terminal transition. The agent can then modify the standard task rewards to define its own reward function, which provably drives it to learn how to achieve all reachable internal goals, and the value of doing so in the current task. We demonstrate two key benefits of WVFs in the context of learning and planning. In particular, given a learned WVF, an agent can compute the optimal policy in a new task by simply estimating the task's reward function. Furthermore, we show that WVFs also implicitly encode the transition dynamics of the environment, and so can be used to perform planning. Experimental results show that WVFs can be learned faster than regular value functions, while their ability to infer the environment's dynamics can be used to integrate learning and planning methods to further improve sample efficiency.

Skill Machines: Temporal Logic Composition in Reinforcement Learning

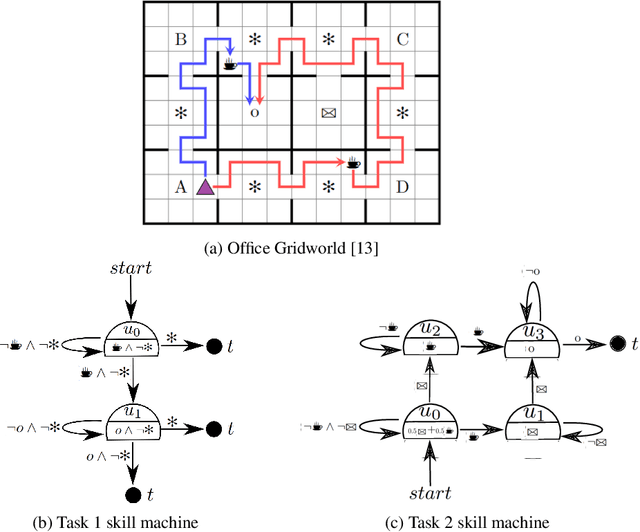
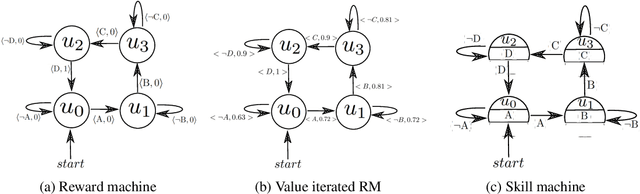
A major challenge in reinforcement learning is specifying tasks in a manner that is both interpretable and verifiable. One common approach is to specify tasks through reward machines -- finite state machines that encode the task to be solved. We introduce skill machines, a representation that can be learned directly from these reward machines that encode the solution to such tasks. We propose a framework where an agent first learns a set of base skills in a reward-free setting, and then combines these skills with the learned skill machine to produce composite behaviours specified by any regular language, such as linear temporal logics. This provides the agent with the ability to map from complex logical task specifications to near-optimal behaviours zero-shot. We demonstrate our approach in both a tabular and high-dimensional video game environment, where an agent is faced with several of these complex, long-horizon tasks. Our results indicate that the agent is capable of satisfying extremely complex task specifications, producing near optimal performance with no further learning. Finally, we demonstrate that the performance of skill machines can be improved with regular offline reinforcement learning algorithms when optimal behaviours are desired.

World Value Functions: Knowledge Representation for Multitask Reinforcement Learning

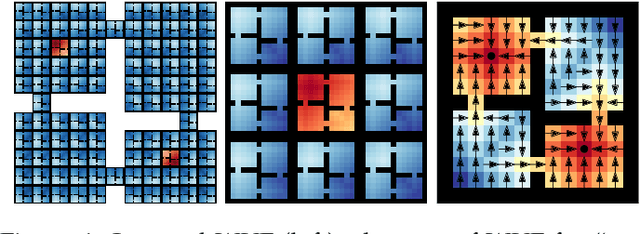
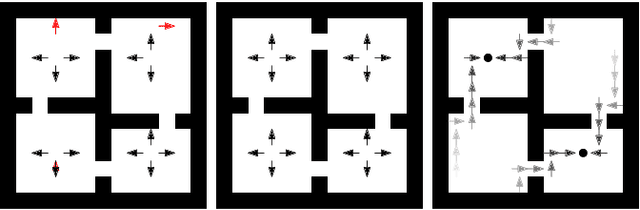
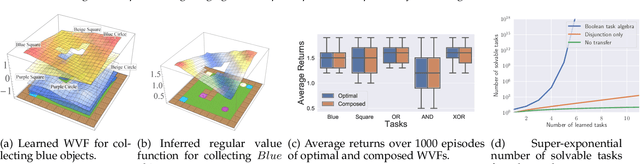
An open problem in artificial intelligence is how to learn and represent knowledge that is sufficient for a general agent that needs to solve multiple tasks in a given world. In this work we propose world value functions (WVFs), which are a type of general value function with mastery of the world - they represent not only how to solve a given task, but also how to solve any other goal-reaching task. To achieve this, we equip the agent with an internal goal space defined as all the world states where it experiences a terminal transition - a task outcome. The agent can then modify task rewards to define its own reward function, which provably drives it to learn how to achieve all achievable internal goals, and the value of doing so in the current task. We demonstrate a number of benefits of WVFs. When the agent's internal goal space is the entire state space, we demonstrate that the transition function can be inferred from the learned WVF, which allows the agent to plan using learned value functions. Additionally, we show that for tasks in the same world, a pretrained agent that has learned any WVF can then infer the policy and value function for any new task directly from its rewards. Finally, an important property for long-lived agents is the ability to reuse existing knowledge to solve new tasks. Using WVFs as the knowledge representation for learned tasks, we show that an agent is able to solve their logical combination zero-shot, resulting in a combinatorially increasing number of skills throughout their lifetime.

Learning to Follow Language Instructions with Compositional Policies

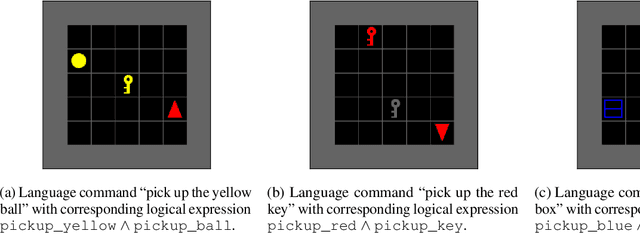
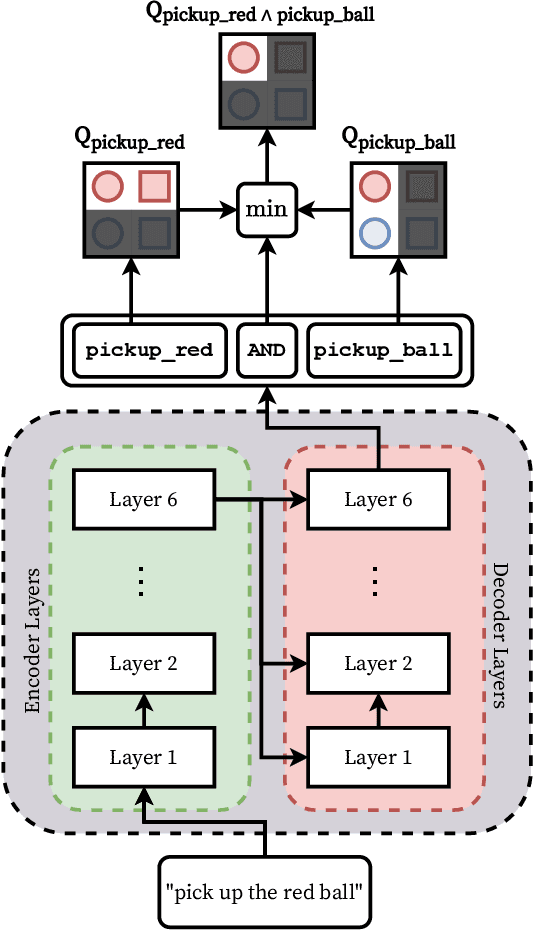
We propose a framework that learns to execute natural language instructions in an environment consisting of goal-reaching tasks that share components of their task descriptions. Our approach leverages the compositionality of both value functions and language, with the aim of reducing the sample complexity of learning novel tasks. First, we train a reinforcement learning agent to learn value functions that can be subsequently composed through a Boolean algebra to solve novel tasks. Second, we fine-tune a seq2seq model pretrained on web-scale corpora to map language to logical expressions that specify the required value function compositions. Evaluating our agent in the BabyAI domain, we observe a decrease of 86% in the number of training steps needed to learn a second task after mastering a single task. Results from ablation studies further indicate that it is the combination of compositional value functions and language representations that allows the agent to quickly generalize to new tasks.

A Boolean Task Algebra for Reinforcement Learning

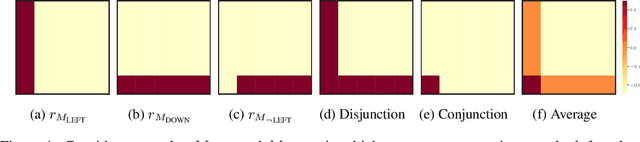
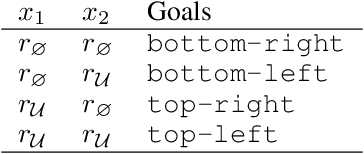
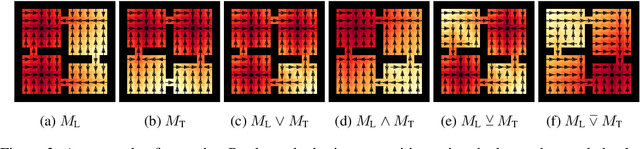
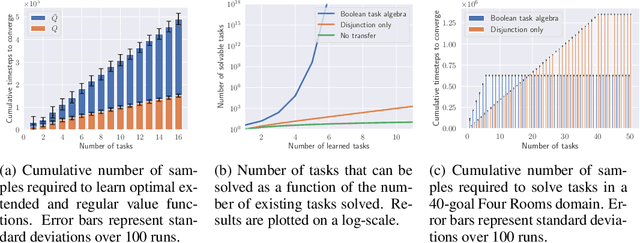
We propose a framework for defining a Boolean algebra over the space of tasks. This allows us to formulate new tasks in terms of the negation, disjunction and conjunction of a set of base tasks. We then show that by learning goal-oriented value functions and restricting the transition dynamics of the tasks, an agent can solve these new tasks with no further learning. We prove that by composing these value functions in specific ways, we immediately recover the optimal policies for all tasks expressible under the Boolean algebra. We verify our approach in two domains, including a high-dimensional video game environment requiring function approximation, where an agent first learns a set of base skills, and then composes them to solve a super-exponential number of new tasks.