A Boolean Task Algebra for Reinforcement Learning
Paper and Code
Jan 06, 2020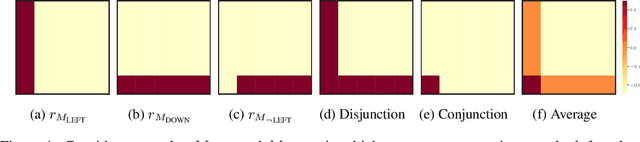
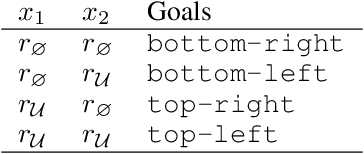
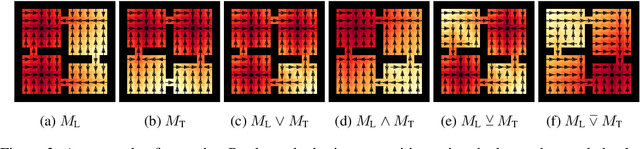
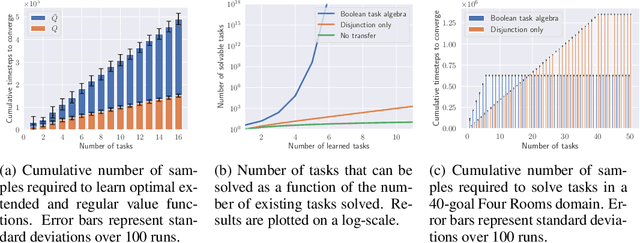
We propose a framework for defining a Boolean algebra over the space of tasks. This allows us to formulate new tasks in terms of the negation, disjunction and conjunction of a set of base tasks. We then show that by learning goal-oriented value functions and restricting the transition dynamics of the tasks, an agent can solve these new tasks with no further learning. We prove that by composing these value functions in specific ways, we immediately recover the optimal policies for all tasks expressible under the Boolean algebra. We verify our approach in two domains, including a high-dimensional video game environment requiring function approximation, where an agent first learns a set of base skills, and then composes them to solve a super-exponential number of new tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge