Super-resolution in disordered media using neural networks

We propose a methodology that exploits large and diverse data sets to accurately estimate the ambient medium's Green's functions in strongly scattering media. Given these estimates, obtained with and without the use of neural networks, excellent imaging results are achieved, with a resolution that is better than that of a homogeneous medium. This phenomenon, also known as super-resolution, occurs because the ambient scattering medium effectively enhances the physical imaging aperture.

Quantitative phase and absorption contrast imaging

Phase retrieval in its most general form is the problem of reconstructing a complex valued function from phaseless information of some transform of that function. This problem arises in various fields such as X-ray crystallography, electron microscopy, coherent diffractive imaging, astronomy, speech recognition, and quantum mechanics. The mathematical and computational analysis of these problems has a long history and a variety of different algorithms has been proposed in the literature. The performance of which usually depends on the constraints imposed on the sought function and the number of measurements. In this paper, we present an algorithm for coherent diffractive imaging with phaseless measurements. The algorithm accounts for both coherent and incoherent wave propagation and allows for reconstructing absorption as well as phase images that quantify the attenuation and the refraction of the waves when they go through an object. The algorithm requires coherent or partially coherent illumination, and several detectors to record the intensity of the distorted wave that passes through the object under inspection. To obtain enough information for imaging, a series of masks are introduced between the source and the object that create a diversity of illumination patterns.

Correlation based Imaging for rotating satellites

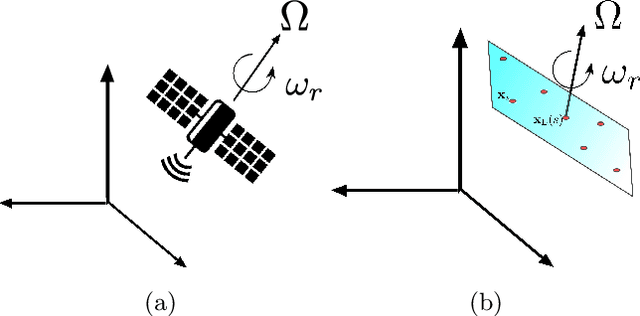
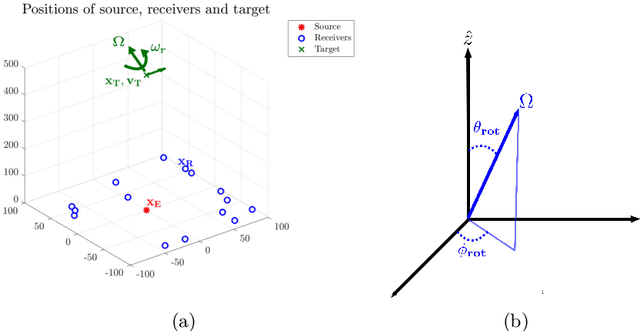
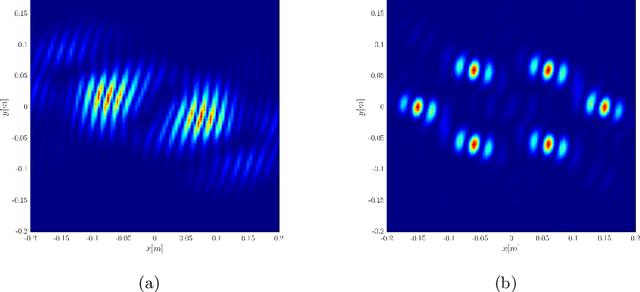
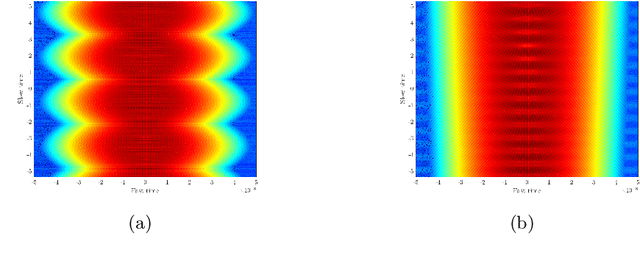
We consider imaging of fast moving small objects in space, such as low earth orbit satellites, which are also rotating around a fixed axis. The imaging system consists of ground based, asynchronous sources of radiation and several passive receivers above the dense atmosphere. We use the cross-correlation of the received signals to reduce distortions from ambient medium fluctuations. Imaging with correlations also has the advantage of not requiring any knowledge about the probing pulse and depends weakly on the emitter positions. We account for the target's orbital velocity by introducing the necessary Doppler compensation. To image a fast rotating object we also need to compensate for the rotation. We show that the rotation parameters can be extracted directly from the auto-correlation of the data before the formation of the image. We then investigate and analyze an imaging method that relies on backpropagating the cross-correlation data structure to two points rather than one, thus forming an interference matrix. The proposed imaging method consists of estimating the reflectivity as the top eigenvector of the migrated cross-correlation data interference matrix. We call this the rank-1 image and show that it provides superior image resolution compared to the usual single-point migration scheme for fast moving and rotating objects. Moreover, we observe a significant improvement in resolution due to the rotation leading to a diffraction limited resolution. We carry out a theoretical analysis that illustrates the role of the two point migration method as well as that of the inverse aperture and rotation in improving resolution. Extensive numerical simulations support the theoretical results.

Fast signal recovery from quadratic measurements

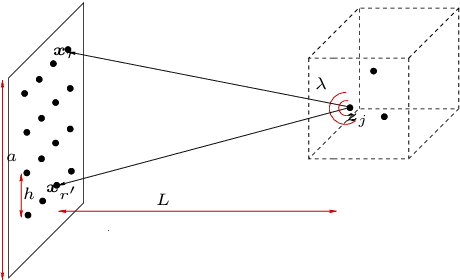
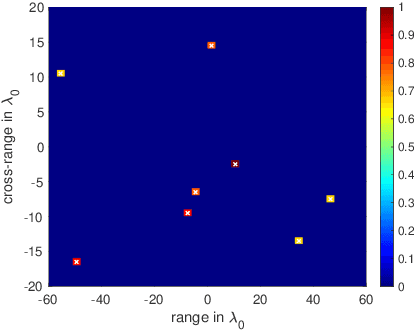
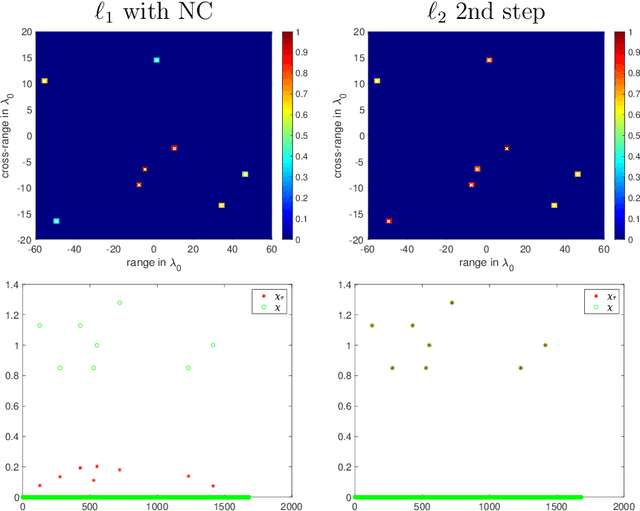
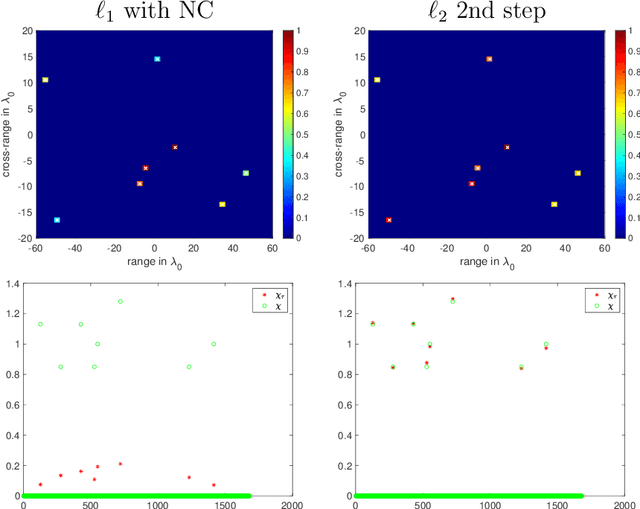
We present a novel approach for recovering a sparse signal from cross-correlated data. Cross-correlations naturally arise in many fields of imaging, such as optics, holography and seismic interferometry. Compared to the sparse signal recovery problem that uses linear measurements, the unknown is now a matrix formed by the cross correlation of the unknown signal. Hence, the bottleneck for inversion is the number of unknowns that grows quadratically. The main idea of our proposed approach is to reduce the dimensionality of the problem by recovering only the diagonal of the unknown matrix, whose dimension grows linearly with the size of the problem. The keystone of the methodology is the use of an efficient {\em Noise Collector} that absorbs the data that come from the off-diagonal elements of the unknown matrix and that do not carry extra information about the support of the signal. This results in a linear problem whose cost is similar to the one that uses linear measurements. Our theory shows that the proposed approach provides exact support recovery when the data is not too noisy, and that there are no false positives for any level of noise. Moreover, our theory also demonstrates that when using cross-correlated data, the level of sparsity that can be recovered increases, scaling almost linearly with the number of data. The numerical experiments presented in the paper corroborate these findings.

The Noise Collector for sparse recovery in high dimensions

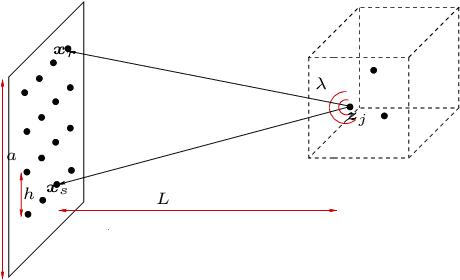
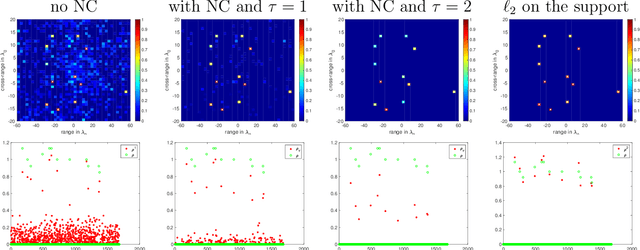
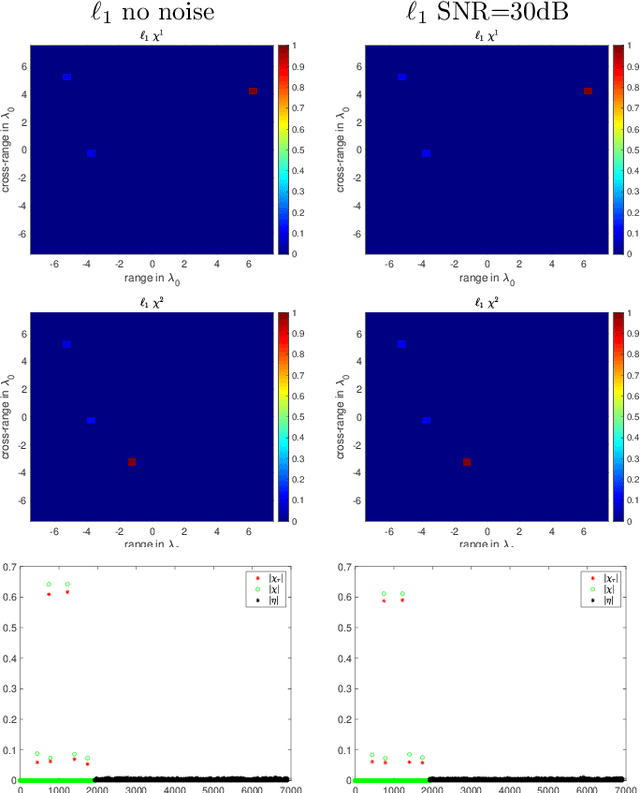
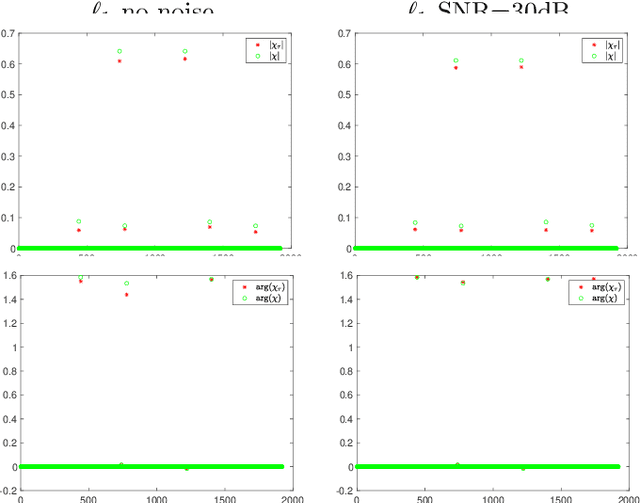
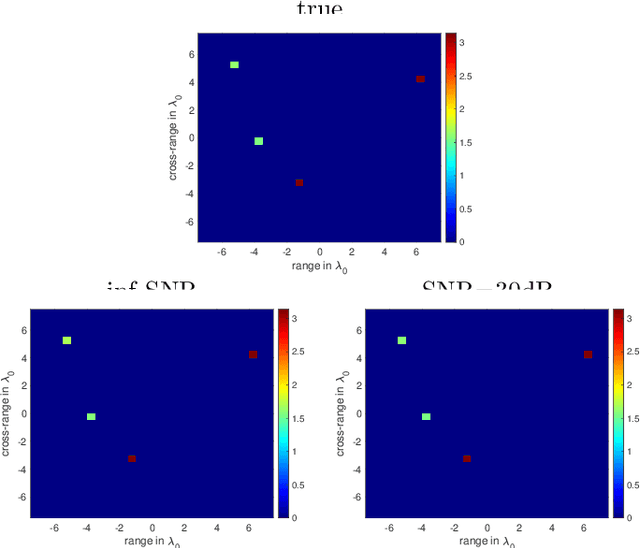
The ability to detect sparse signals from noisy high-dimensional data is a top priority in modern science and engineering. A sparse solution of the linear system $A \rho = b_0$ can be found efficiently with an $l_1$-norm minimization approach if the data is noiseless. Detection of the signal's support from data corrupted by noise is still a challenging problem, especially if the level of noise must be estimated. We propose a new efficient approach that does not require any parameter estimation. We introduce the Noise Collector (NC) matrix $C$ and solve an augmented system $A \rho + C \eta = b_0 + e$, where $ e$ is the noise. We show that the $l_1$-norm minimal solution of the augmented system has zero false discovery rate for any level of noise and with probability that tends to one as the dimension of $ b_0$ increases to infinity. We also obtain exact support recovery if the noise is not too large, and develop a Fast Noise Collector Algorithm which makes the computational cost of solving the augmented system comparable to that of the original one. Finally, we demonstrate the effectiveness of the method in applications to passive array imaging.

Imaging with highly incomplete and corrupted data

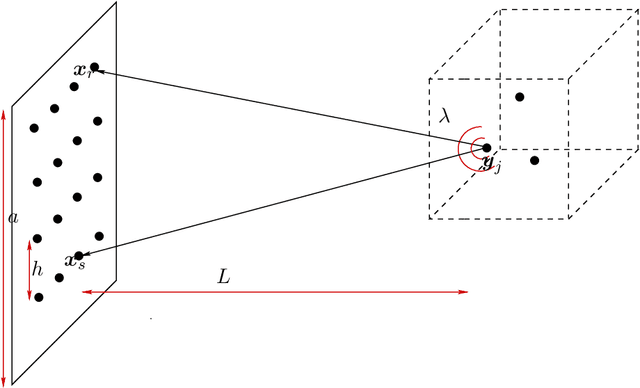
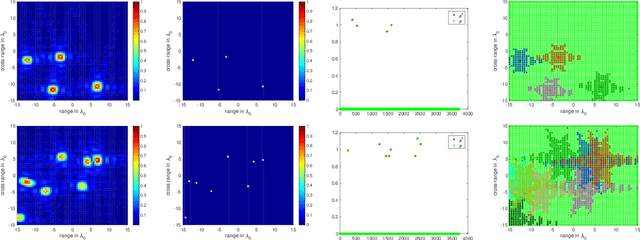
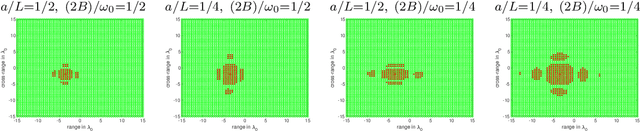
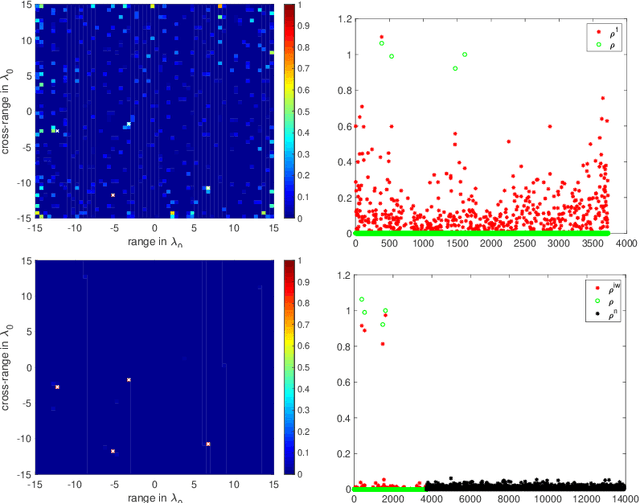
We consider the problem of imaging sparse scenes from a few noisy data using an $l_1$-minimization approach. This problem can be cast as a linear system of the form $A \, \rho =b$, where $A$ is an $N\times K$ measurement matrix. We assume that the dimension of the unknown sparse vector $\rho \in {\mathbb{C}}^K$ is much larger than the dimension of the data vector $b \in {\mathbb{C}}^N$, i.e, $K \gg N$. We provide a theoretical framework that allows us to examine under what conditions the $\ell_1$-minimization problem admits a solution that is close to the exact one in the presence of noise. Our analysis shows that $l_1$-minimization is not robust for imaging with noisy data when high resolution is required. To improve the performance of $l_1$-minimization we propose to solve instead the augmented linear system $ [A \, | \, C] \rho =b$, where the $N \times \Sigma$ matrix $C$ is a noise collector. It is constructed so as its column vectors provide a frame on which the noise of the data, a vector of dimension $N$, can be well approximated. Theoretically, the dimension $\Sigma$ of the noise collector should be $e^N$ which would make its use not practical. However, our numerical results illustrate that robust results in the presence of noise can be obtained with a large enough number of columns $\Sigma \approx 10 K$.