Fast signal recovery from quadratic measurements

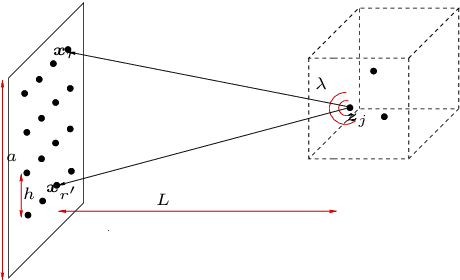
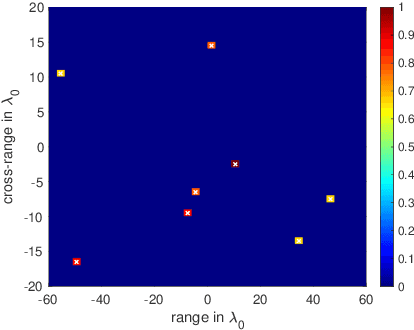
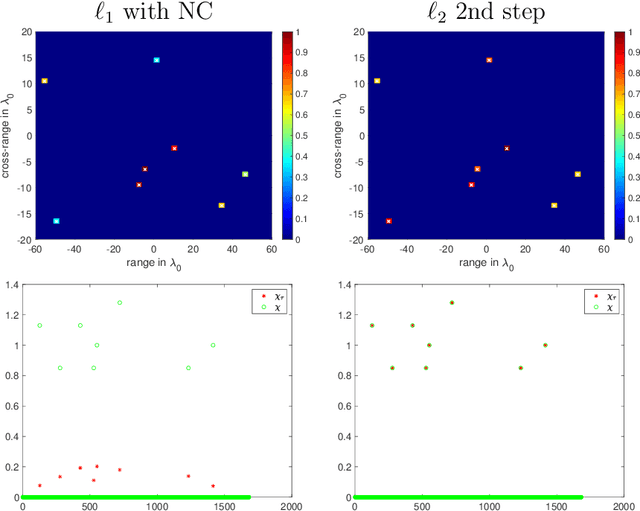
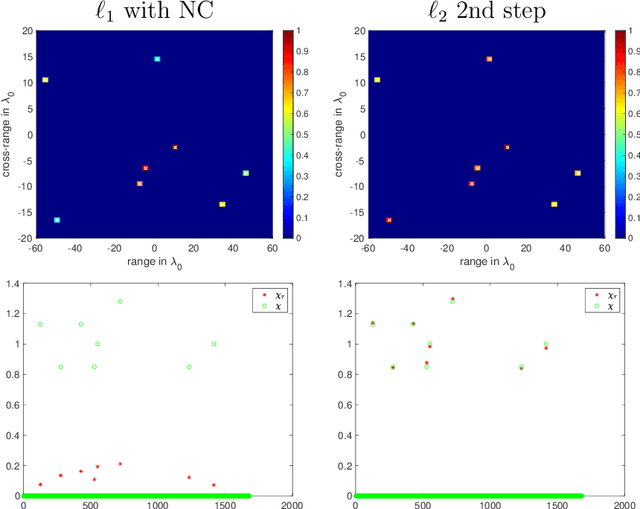
We present a novel approach for recovering a sparse signal from cross-correlated data. Cross-correlations naturally arise in many fields of imaging, such as optics, holography and seismic interferometry. Compared to the sparse signal recovery problem that uses linear measurements, the unknown is now a matrix formed by the cross correlation of the unknown signal. Hence, the bottleneck for inversion is the number of unknowns that grows quadratically. The main idea of our proposed approach is to reduce the dimensionality of the problem by recovering only the diagonal of the unknown matrix, whose dimension grows linearly with the size of the problem. The keystone of the methodology is the use of an efficient {\em Noise Collector} that absorbs the data that come from the off-diagonal elements of the unknown matrix and that do not carry extra information about the support of the signal. This results in a linear problem whose cost is similar to the one that uses linear measurements. Our theory shows that the proposed approach provides exact support recovery when the data is not too noisy, and that there are no false positives for any level of noise. Moreover, our theory also demonstrates that when using cross-correlated data, the level of sparsity that can be recovered increases, scaling almost linearly with the number of data. The numerical experiments presented in the paper corroborate these findings.