Quantitative phase and absorption contrast imaging

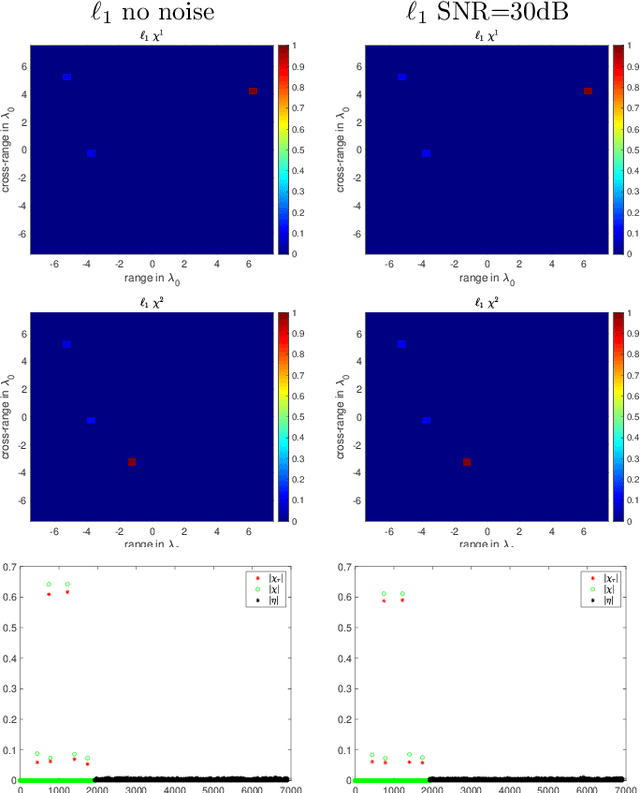
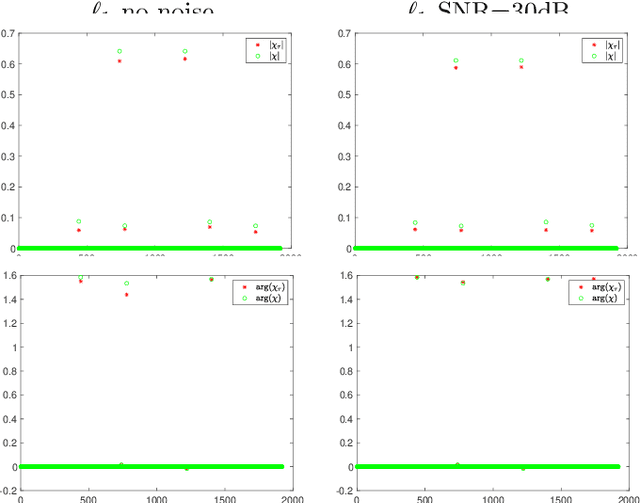
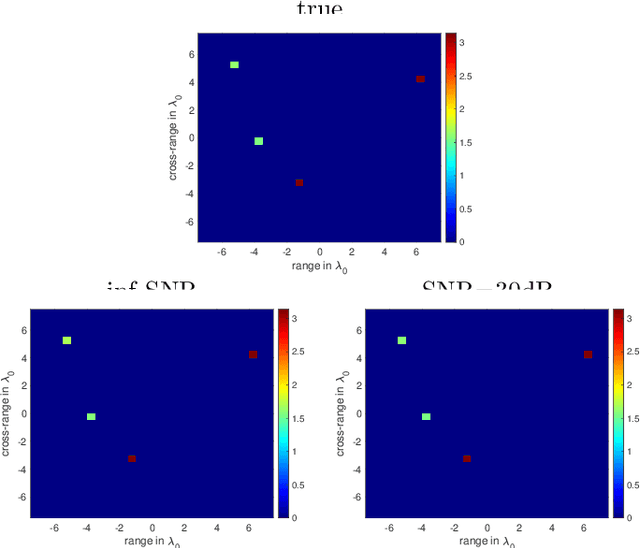
Phase retrieval in its most general form is the problem of reconstructing a complex valued function from phaseless information of some transform of that function. This problem arises in various fields such as X-ray crystallography, electron microscopy, coherent diffractive imaging, astronomy, speech recognition, and quantum mechanics. The mathematical and computational analysis of these problems has a long history and a variety of different algorithms has been proposed in the literature. The performance of which usually depends on the constraints imposed on the sought function and the number of measurements. In this paper, we present an algorithm for coherent diffractive imaging with phaseless measurements. The algorithm accounts for both coherent and incoherent wave propagation and allows for reconstructing absorption as well as phase images that quantify the attenuation and the refraction of the waves when they go through an object. The algorithm requires coherent or partially coherent illumination, and several detectors to record the intensity of the distorted wave that passes through the object under inspection. To obtain enough information for imaging, a series of masks are introduced between the source and the object that create a diversity of illumination patterns.