The Noise Collector for sparse recovery in high dimensions
Paper and Code
Aug 05, 2019

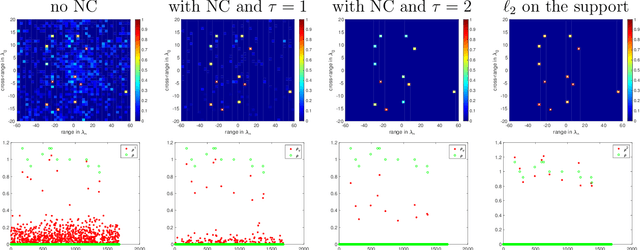
The ability to detect sparse signals from noisy high-dimensional data is a top priority in modern science and engineering. A sparse solution of the linear system $A \rho = b_0$ can be found efficiently with an $l_1$-norm minimization approach if the data is noiseless. Detection of the signal's support from data corrupted by noise is still a challenging problem, especially if the level of noise must be estimated. We propose a new efficient approach that does not require any parameter estimation. We introduce the Noise Collector (NC) matrix $C$ and solve an augmented system $A \rho + C \eta = b_0 + e$, where $ e$ is the noise. We show that the $l_1$-norm minimal solution of the augmented system has zero false discovery rate for any level of noise and with probability that tends to one as the dimension of $ b_0$ increases to infinity. We also obtain exact support recovery if the noise is not too large, and develop a Fast Noise Collector Algorithm which makes the computational cost of solving the augmented system comparable to that of the original one. Finally, we demonstrate the effectiveness of the method in applications to passive array imaging.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge