Imaging with highly incomplete and corrupted data
Paper and Code
Aug 05, 2019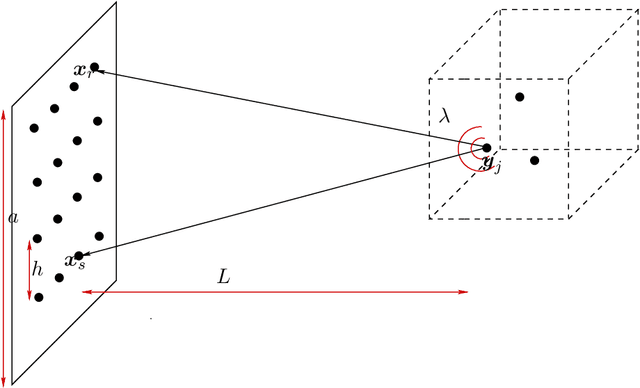
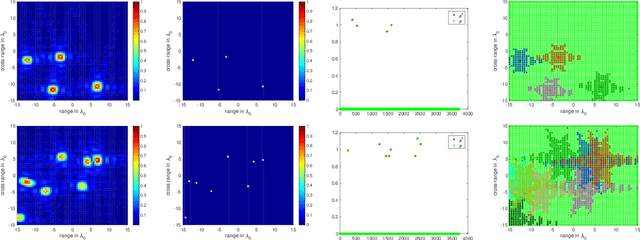
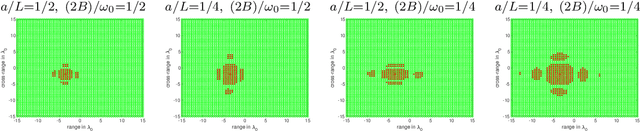
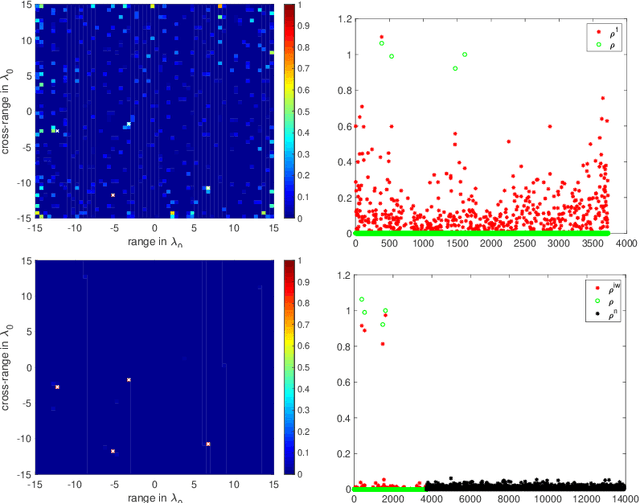
We consider the problem of imaging sparse scenes from a few noisy data using an $l_1$-minimization approach. This problem can be cast as a linear system of the form $A \, \rho =b$, where $A$ is an $N\times K$ measurement matrix. We assume that the dimension of the unknown sparse vector $\rho \in {\mathbb{C}}^K$ is much larger than the dimension of the data vector $b \in {\mathbb{C}}^N$, i.e, $K \gg N$. We provide a theoretical framework that allows us to examine under what conditions the $\ell_1$-minimization problem admits a solution that is close to the exact one in the presence of noise. Our analysis shows that $l_1$-minimization is not robust for imaging with noisy data when high resolution is required. To improve the performance of $l_1$-minimization we propose to solve instead the augmented linear system $ [A \, | \, C] \rho =b$, where the $N \times \Sigma$ matrix $C$ is a noise collector. It is constructed so as its column vectors provide a frame on which the noise of the data, a vector of dimension $N$, can be well approximated. Theoretically, the dimension $\Sigma$ of the noise collector should be $e^N$ which would make its use not practical. However, our numerical results illustrate that robust results in the presence of noise can be obtained with a large enough number of columns $\Sigma \approx 10 K$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge