Gradient Monitored Reinforcement Learning

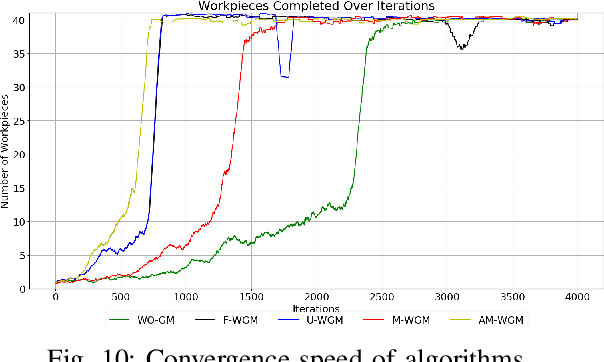
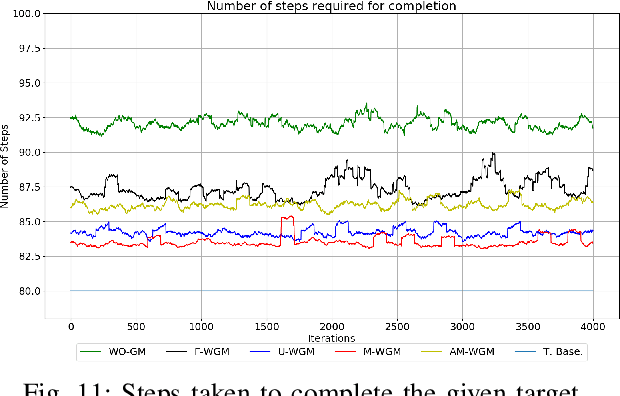
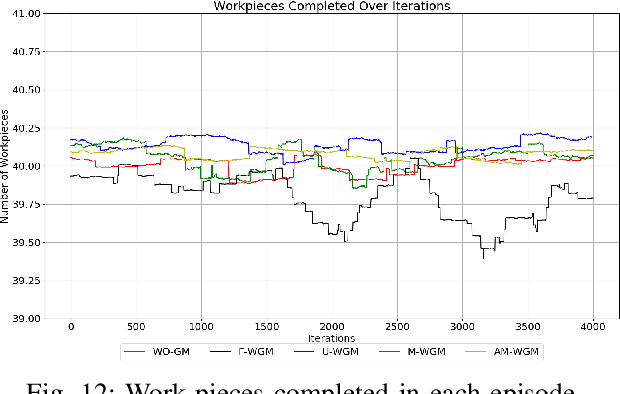
This paper presents a novel neural network training approach for faster convergence and better generalization abilities in deep reinforcement learning. Particularly, we focus on the enhancement of training and evaluation performance in reinforcement learning algorithms by systematically reducing gradient's variance and thereby providing a more targeted learning process. The proposed method which we term as Gradient Monitoring(GM), is an approach to steer the learning in the weight parameters of a neural network based on the dynamic development and feedback from the training process itself. We propose different variants of the GM methodology which have been proven to increase the underlying performance of the model. The one of the proposed variant, Momentum with Gradient Monitoring (M-WGM), allows for a continuous adjustment of the quantum of back-propagated gradients in the network based on certain learning parameters. We further enhance the method with Adaptive Momentum with Gradient Monitoring (AM-WGM) method which allows for automatic adjustment between focused learning of certain weights versus a more dispersed learning depending on the feedback from the rewards collected. As a by-product, it also allows for automatic derivation of the required deep network sizes during training as the algorithm automatically freezes trained weights. The approach is applied to two discrete (Multi-Robot Co-ordination problem and Atari games) and one continuous control task (MuJoCo) using Advantage Actor-Critic (A2C) and Proximal Policy Optimization (PPO) respectively. The results obtained particularly underline the applicability and performance improvements of the methods in terms of generalization capability.

Learning the Non-linearity in Convolutional Neural Networks

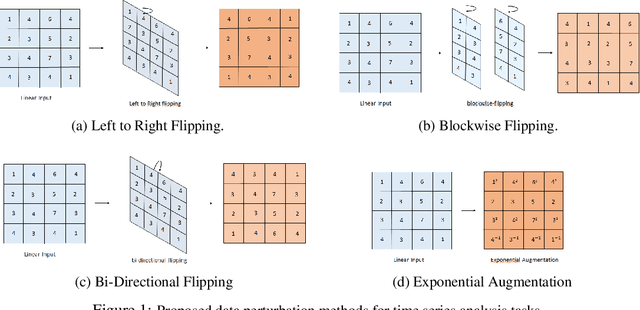
We propose the introduction of nonlinear operation into the feature generation process in convolutional neural networks. This nonlinearity can be implemented in various ways. First we discuss the use of nonlinearities in the process of data augmentation to increase the robustness of the neural networks recognition capacity. To this end, we randomly disturb the input data set by applying exponents within a certain numerical range to individual data points of the input space. Second we propose nonlinear convolutional neural networks where we apply the exponential operation to each element of the receptive field. To this end, we define an additional weight matrix of the same dimension as the standard kernel weight matrix. The weights of this matrix then constitute the exponents of the corresponding components of the receptive field. In the basic setting, we keep the weight parameters fixed during training by defining suitable parameters. Alternatively, we make the exponential weight parameters end-to-end trainable using a suitable parameterization. The network architecture is applied to time series analysis data set showing a considerable increase in the classification performance compared to baseline networks.

Generalized Dilation Neural Networks

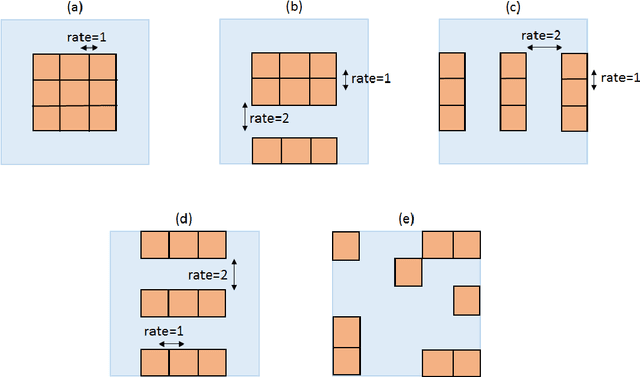
Vanilla convolutional neural networks are known to provide superior performance not only in image recognition tasks but also in natural language processing and time series analysis. One of the strengths of convolutional layers is the ability to learn features about spatial relations in the input domain using various parameterized convolutional kernels. However, in time series analysis learning such spatial relations is not necessarily required nor effective. In such cases, kernels which model temporal dependencies or kernels with broader spatial resolutions are recommended for more efficient training as proposed by dilation kernels. However, the dilation has to be fixed a priori which limits the flexibility of the kernels. We propose generalized dilation networks which generalize the initial dilations in two aspects. First we derive an end-to-end learnable architecture for dilation layers where also the dilation rate can be learned. Second we break up the strict dilation structure, in that we develop kernels operating independently in the input space.