Learning the Non-linearity in Convolutional Neural Networks

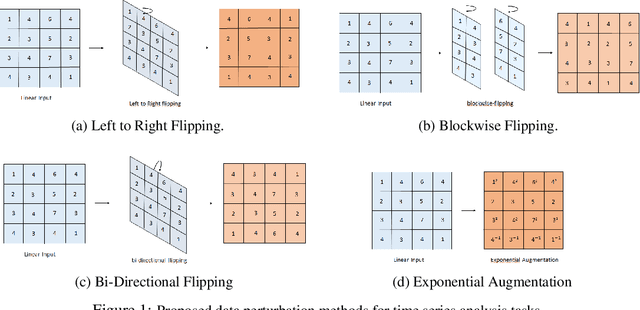
We propose the introduction of nonlinear operation into the feature generation process in convolutional neural networks. This nonlinearity can be implemented in various ways. First we discuss the use of nonlinearities in the process of data augmentation to increase the robustness of the neural networks recognition capacity. To this end, we randomly disturb the input data set by applying exponents within a certain numerical range to individual data points of the input space. Second we propose nonlinear convolutional neural networks where we apply the exponential operation to each element of the receptive field. To this end, we define an additional weight matrix of the same dimension as the standard kernel weight matrix. The weights of this matrix then constitute the exponents of the corresponding components of the receptive field. In the basic setting, we keep the weight parameters fixed during training by defining suitable parameters. Alternatively, we make the exponential weight parameters end-to-end trainable using a suitable parameterization. The network architecture is applied to time series analysis data set showing a considerable increase in the classification performance compared to baseline networks.