Predicting Wall Thickness Changes in Cold Forging Processes: An Integrated FEM and Neural Network approach

This study presents a novel approach for predicting wall thickness changes in tubes during the nosing process. Specifically, we first provide a thorough analysis of nosing processes and the influencing parameters. We further set-up a Finite Element Method (FEM) simulation to better analyse the effects of varying process parameters. As however traditional FEM simulations, while accurate, are time-consuming and computationally intensive, which renders them inapplicable for real-time application, we present a novel modeling framework based on specifically designed graph neural networks as surrogate models. To this end, we extend the neural network architecture by directly incorporating information about the nosing process by adding different types of edges and their corresponding encoders to model object interactions. This augmentation enhances model accuracy and opens the possibility for employing precise surrogate models within closed-loop production processes. The proposed approach is evaluated using a new evaluation metric termed area between thickness curves (ABTC). The results demonstrate promising performance and highlight the potential of neural networks as surrogate models in predicting wall thickness changes during nosing forging processes.

Neural Logic Rule Layers

Despite their great success in recent years, deep neural networks (DNN) are mainly black boxes where the results obtained by running through the network are difficult to understand and interpret. Compared to e.g. decision trees or bayesian classifiers, DNN suffer from bad interpretability where we understand by interpretability, that a human can easily derive the relations modeled by the network. A reasonable way to provide interpretability for humans are logical rules. In this paper we propose neural logic rule layers (NLRL) which are able to represent arbitrary logic rules in terms of their conjunctive and disjunctive normal forms. Using various NLRL within one layer and correspondingly stacking various layers, we are able to represent arbitrary complex rules by the resulting neural network architecture. The NLRL are end-to-end trainable allowing to learn logic rules directly from available data sets. Experiments show that NLRL-enhanced neural networks can learn to model arbitrary complex logic and perform arithmetic operation over the input values.

Generalized Dilation Neural Networks

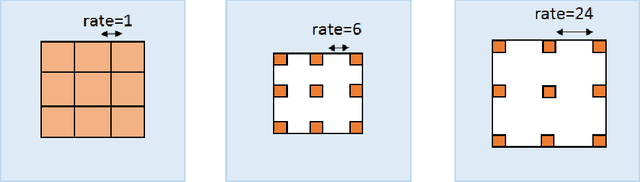
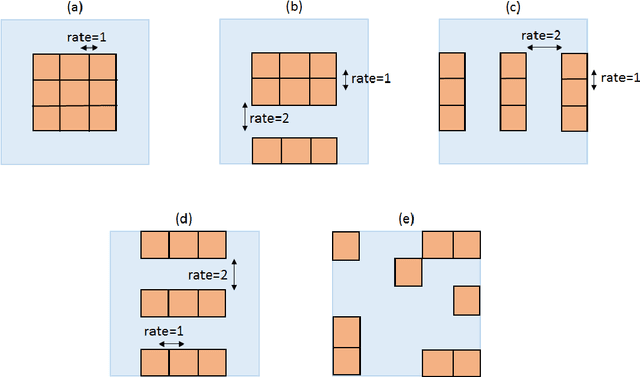
Vanilla convolutional neural networks are known to provide superior performance not only in image recognition tasks but also in natural language processing and time series analysis. One of the strengths of convolutional layers is the ability to learn features about spatial relations in the input domain using various parameterized convolutional kernels. However, in time series analysis learning such spatial relations is not necessarily required nor effective. In such cases, kernels which model temporal dependencies or kernels with broader spatial resolutions are recommended for more efficient training as proposed by dilation kernels. However, the dilation has to be fixed a priori which limits the flexibility of the kernels. We propose generalized dilation networks which generalize the initial dilations in two aspects. First we derive an end-to-end learnable architecture for dilation layers where also the dilation rate can be learned. Second we break up the strict dilation structure, in that we develop kernels operating independently in the input space.