Predicting Wall Thickness Changes in Cold Forging Processes: An Integrated FEM and Neural Network approach

This study presents a novel approach for predicting wall thickness changes in tubes during the nosing process. Specifically, we first provide a thorough analysis of nosing processes and the influencing parameters. We further set-up a Finite Element Method (FEM) simulation to better analyse the effects of varying process parameters. As however traditional FEM simulations, while accurate, are time-consuming and computationally intensive, which renders them inapplicable for real-time application, we present a novel modeling framework based on specifically designed graph neural networks as surrogate models. To this end, we extend the neural network architecture by directly incorporating information about the nosing process by adding different types of edges and their corresponding encoders to model object interactions. This augmentation enhances model accuracy and opens the possibility for employing precise surrogate models within closed-loop production processes. The proposed approach is evaluated using a new evaluation metric termed area between thickness curves (ABTC). The results demonstrate promising performance and highlight the potential of neural networks as surrogate models in predicting wall thickness changes during nosing forging processes.

Improving Quaternion Neural Networks with Quaternionic Activation Functions

In this paper, we propose novel quaternion activation functions where we modify either the quaternion magnitude or the phase, as an alternative to the commonly used split activation functions. We define criteria that are relevant for quaternion activation functions, and subsequently we propose our novel activation functions based on this analysis. Instead of applying a known activation function like the ReLU or Tanh on the quaternion elements separately, these activation functions consider the quaternion properties and respect the quaternion space $\mathbb{H}$. In particular, all quaternion components are utilized to calculate all output components, carrying out the benefit of the Hamilton product in e.g. the quaternion convolution to the activation functions. The proposed activation functions can be incorporated in arbitrary quaternion valued neural networks trained with gradient descent techniques. We further discuss the derivatives of the proposed activation functions where we observe beneficial properties for the activation functions affecting the phase. Specifically, they prove to be sensitive on basically the whole input range, thus improved gradient flow can be expected. We provide an elaborate experimental evaluation of our proposed quaternion activation functions including comparison with the split ReLU and split Tanh on two image classification tasks using the CIFAR-10 and SVHN dataset. There, especially the quaternion activation functions affecting the phase consistently prove to provide better performance.

Time Series Compression using Quaternion Valued Neural Networks and Quaternion Backpropagation

We propose a novel quaternionic time-series compression methodology where we divide a long time-series into segments of data, extract the min, max, mean and standard deviation of these chunks as representative features and encapsulate them in a quaternion, yielding a quaternion valued time-series. This time-series is processed using quaternion valued neural network layers, where we aim to preserve the relation between these features through the usage of the Hamilton product. To train this quaternion neural network, we derive quaternion backpropagation employing the GHR calculus, which is required for a valid product and chain rule in quaternion space. Furthermore, we investigate the connection between the derived update rules and automatic differentiation. We apply our proposed compression method on the Tennessee Eastman Dataset, where we perform fault classification using the compressed data in two settings: a fully supervised one and in a semi supervised, contrastive learning setting. Both times, we were able to outperform real valued counterparts as well as two baseline models: one with the uncompressed time-series as the input and the other with a regular downsampling using the mean. Further, we could improve the classification benchmark set by SimCLR-TS from 81.43% to 83.90%.

Quaternion Backpropagation

Quaternion valued neural networks experienced rising popularity and interest from researchers in the last years, whereby the derivatives with respect to quaternions needed for optimization are calculated as the sum of the partial derivatives with respect to the real and imaginary parts. However, we can show that product- and chain-rule does not hold with this approach. We solve this by employing the GHRCalculus and derive quaternion backpropagation based on this. Furthermore, we experimentally prove the functionality of the derived quaternion backpropagation.

Predicting Rigid Body Dynamics using Dual Quaternion Recurrent Neural Networks with Quaternion Attention

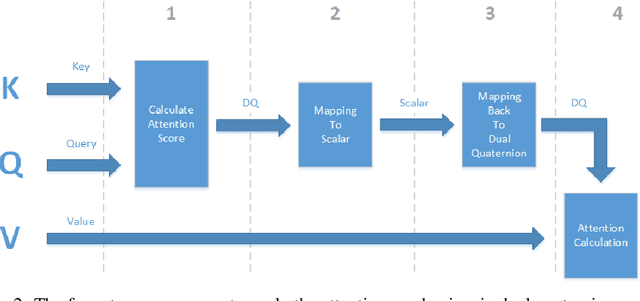
We propose a novel neural network architecture based on dual quaternions which allow for a compact representation of informations with a main focus on describing rigid body movements. To cover the dynamic behavior inherent to rigid body movements, we propose recurrent architectures in the neural network. To further model the interactions between individual rigid bodies as well as external inputs efficiently, we incorporate a novel attention mechanism employing dual quaternion algebra. The introduced architecture is trainable by means of gradient based algorithms. We apply our approach to a parcel prediction problem where a rigid body with an initial position, orientation, velocity and angular velocity moves through a fixed simulation environment which exhibits rich interactions between the parcel and the boundaries.