Francois Lauze
Deep Learning-Assisted Localisation of Nanoparticles in synthetically generated two-photon microscopy images
Mar 17, 2023Abstract:Tracking single molecules is instrumental for quantifying the transport of molecules and nanoparticles in biological samples, e.g., in brain drug delivery studies. Existing intensity-based localisation methods are not developed for imaging with a scanning microscope, typically used for in vivo imaging. Low signal-to-noise ratios, movement of molecules out-of-focus, and high motion blur on images recorded with scanning two-photon microscopy (2PM) in vivo pose a challenge to the accurate localisation of molecules. Using data-driven models is challenging due to low data volumes, typical for in vivo experiments. We developed a 2PM image simulator to supplement scarce training data. The simulator mimics realistic motion blur, background fluorescence, and shot noise observed in vivo imaging. Training a data-driven model with simulated data improves localisation quality in simulated images and shows why intensity-based methods fail.
First Order Locally Orderless Registration
Aug 10, 2021


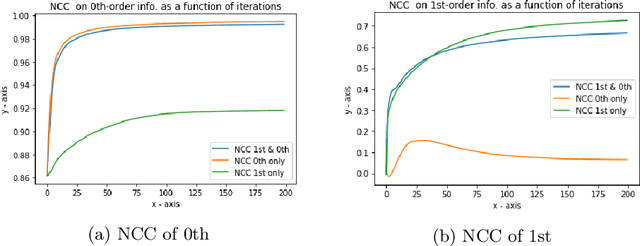
Abstract:First Order Locally Orderless Registration (FLOR) is a scale-space framework for image density estimation used for defining image similarity, mainly for Image Registration. The Locally Orderless Registration framework was designed in principle to use zeroth-order information, providing image density estimates over three scales: image scale, intensity scale, and integration scale. We extend it to take first-order information into account and hint at higher-order information. We show how standard similarity measures extend into the framework. We study especially Sum of Squared Differences (SSD) and Normalized Cross-Correlation (NCC) but present the theory of how Normalised Mutual Information (NMI) can be included.
On Variational Methods for Motion Compensated Inpainting
Sep 21, 2018


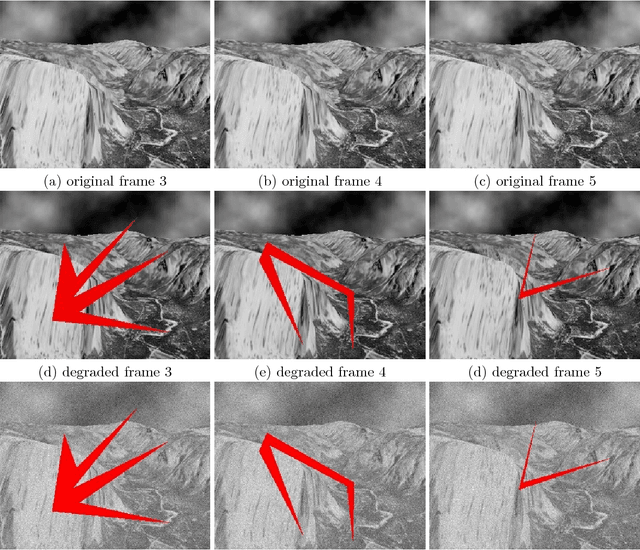
Abstract:We develop in this paper a generic Bayesian framework for the joint estimation of motion and recovery of missing data in a damaged video sequence. Using standard maximum a posteriori to variational formulation rationale, we derive generic minimum energy formulations for the estimation of a reconstructed sequence as well as motion recovery. We instantiate these energy formulations and from their Euler-Lagrange Equations, we propose a full multiresolution algorithms in order to compute good local minimizers for our energies and discuss their numerical implementations, focusing on the missing data recovery part, i.e. inpainting. Experimental results for synthetic as well as real sequences are presented. Image sequences and extra material is available at http://image.diku.dk/francois/seqinp.php.
Geodesic Exponential Kernels: When Curvature and Linearity Conflict
Nov 17, 2014
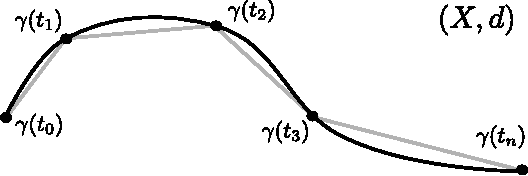


Abstract:We consider kernel methods on general geodesic metric spaces and provide both negative and positive results. First we show that the common Gaussian kernel can only be generalized to a positive definite kernel on a geodesic metric space if the space is flat. As a result, for data on a Riemannian manifold, the geodesic Gaussian kernel is only positive definite if the Riemannian manifold is Euclidean. This implies that any attempt to design geodesic Gaussian kernels on curved Riemannian manifolds is futile. However, we show that for spaces with conditionally negative definite distances the geodesic Laplacian kernel can be generalized while retaining positive definiteness. This implies that geodesic Laplacian kernels can be generalized to some curved spaces, including spheres and hyperbolic spaces. Our theoretical results are verified empirically.
Towards a theory of statistical tree-shape analysis
Jul 23, 2012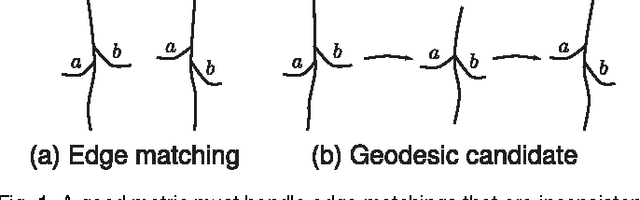
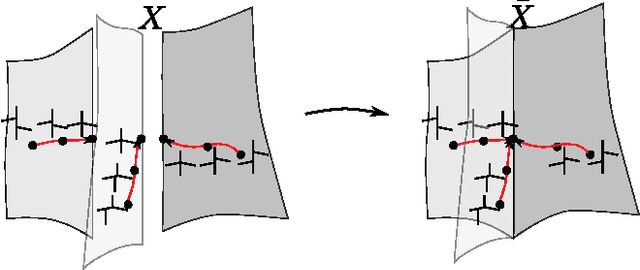
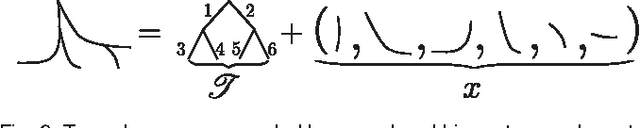

Abstract:In order to develop statistical methods for shapes with a tree-structure, we construct a shape space framework for tree-like shapes and study metrics on the shape space. This shape space has singularities, corresponding to topological transitions in the represented trees. We study two closely related metrics on the shape space, TED and QED. QED is a quotient Euclidean distance arising naturally from the shape space formulation, while TED is the classical tree edit distance. Using Gromov's metric geometry we gain new insight into the geometries defined by TED and QED. We show that the new metric QED has nice geometric properties which facilitate statistical analysis, such as existence and local uniqueness of geodesics and averages. TED, on the other hand, does not share the geometric advantages of QED, but has nice algorithmic properties. We provide a theoretical framework and experimental results on synthetic data trees as well as airway trees from pulmonary CT scans. This way, we effectively illustrate that our framework has both the theoretical and qualitative properties necessary to build a theory of statistical tree-shape analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge