Kid-Net: Convolution Networks for Kidney Vessels Segmentation from CT-Volumes

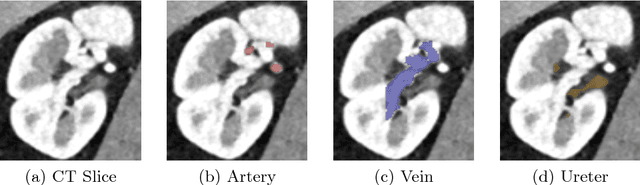
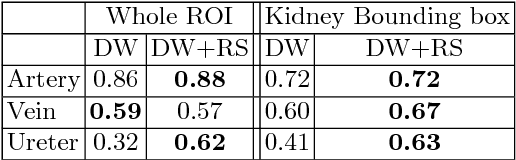
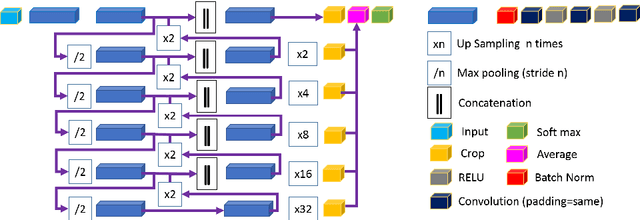
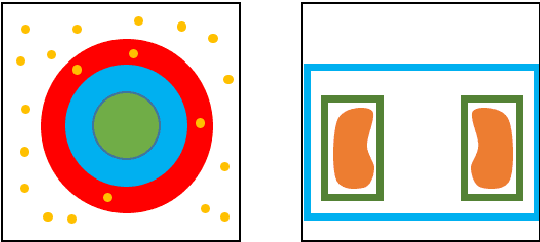
Semantic image segmentation plays an important role in modeling patient-specific anatomy. We propose a convolution neural network, called Kid-Net, along with a training schema to segment kidney vessels: artery, vein and collecting system. Such segmentation is vital during the surgical planning phase in which medical decisions are made before surgical incision. Our main contribution is developing a training schema that handles unbalanced data, reduces false positives and enables high-resolution segmentation with a limited memory budget. These objectives are attained using dynamic weighting, random sampling and 3D patch segmentation. Manual medical image annotation is both time-consuming and expensive. Kid-Net reduces kidney vessels segmentation time from matter of hours to minutes. It is trained end-to-end using 3D patches from volumetric CT-images. A complete segmentation for a 512x512x512 CT-volume is obtained within a few minutes (1-2 mins) by stitching the output 3D patches together. Feature down-sampling and up-sampling are utilized to achieve higher classification and localization accuracies. Quantitative and qualitative evaluation results on a challenging testing dataset show Kid-Net competence.

Towards a theory of statistical tree-shape analysis

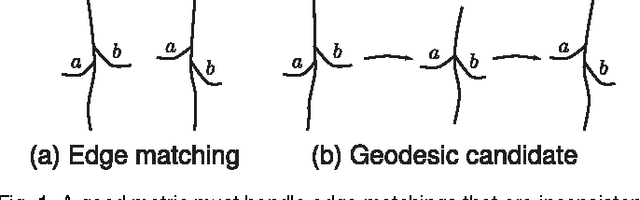
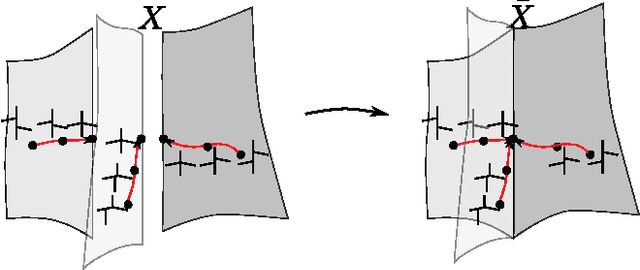
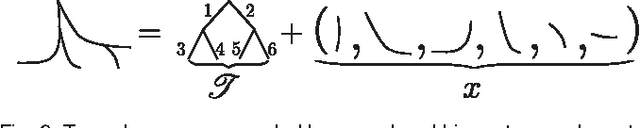
In order to develop statistical methods for shapes with a tree-structure, we construct a shape space framework for tree-like shapes and study metrics on the shape space. This shape space has singularities, corresponding to topological transitions in the represented trees. We study two closely related metrics on the shape space, TED and QED. QED is a quotient Euclidean distance arising naturally from the shape space formulation, while TED is the classical tree edit distance. Using Gromov's metric geometry we gain new insight into the geometries defined by TED and QED. We show that the new metric QED has nice geometric properties which facilitate statistical analysis, such as existence and local uniqueness of geodesics and averages. TED, on the other hand, does not share the geometric advantages of QED, but has nice algorithmic properties. We provide a theoretical framework and experimental results on synthetic data trees as well as airway trees from pulmonary CT scans. This way, we effectively illustrate that our framework has both the theoretical and qualitative properties necessary to build a theory of statistical tree-shape analysis.