Generative Parametric Design (GPD): A framework for real-time geometry generation and on-the-fly multiparametric approximation

This paper presents a novel paradigm in simulation-based engineering sciences by introducing a new framework called Generative Parametric Design (GPD). The GPD framework enables the generation of new designs along with their corresponding parametric solutions given as a reduced basis. To achieve this, two Rank Reduction Autoencoders (RRAEs) are employed, one for encoding and generating the design or geometry, and the other for encoding the sparse Proper Generalized Decomposition (sPGD) mode solutions. These models are linked in the latent space using regression techniques, allowing efficient transitions between design and their associated sPGD modes. By empowering design exploration and optimization, this framework also advances digital and hybrid twin development, enhancing predictive modeling and real-time decision-making in engineering applications. The developed framework is demonstrated on two-phase microstructures, in which the multiparametric solutions account for variations in two key material parameters.

RRAEDy: Adaptive Latent Linearization of Nonlinear Dynamical Systems

Most existing latent-space models for dynamical systems require fixing the latent dimension in advance, they rely on complex loss balancing to approximate linear dynamics, and they don't regularize the latent variables. We introduce RRAEDy, a model that removes these limitations by discovering the appropriate latent dimension, while enforcing both regularized and linearized dynamics in the latent space. Built upon Rank-Reduction Autoencoders (RRAEs), RRAEDy automatically rank and prune latent variables through their singular values while learning a latent Dynamic Mode Decomposition (DMD) operator that governs their temporal progression. This structure-free yet linearly constrained formulation enables the model to learn stable and low-dimensional dynamics without auxiliary losses or manual tuning. We provide theoretical analysis demonstrating the stability of the learned operator and showcase the generality of our model by proposing an extension that handles parametric ODEs. Experiments on canonical benchmarks, including the Van der Pol oscillator, Burgers' equation, 2D Navier-Stokes, and Rotating Gaussians, show that RRAEDy achieves accurate and robust predictions. Our code is open-source and available at https://github.com/JadM133/RRAEDy. We also provide a video summarizing the main results at https://youtu.be/ox70mSSMGrM.

Variational Rank Reduction Autoencoders for Generative Thermal Design

Generative thermal design for complex geometries is fundamental in many areas of engineering, yet it faces two main challenges: the high computational cost of high-fidelity simulations and the limitations of conventional generative models. Approaches such as autoencoders (AEs) and variational autoencoders (VAEs) often produce unstructured latent spaces with discontinuities, which restricts their capacity to explore designs and generate physically consistent solutions. To address these limitations, we propose a hybrid framework that combines Variational Rank-Reduction Autoencoders (VRRAEs) with Deep Operator Networks (DeepONets). The VRRAE introduces a truncated SVD within the latent space, leading to continuous, interpretable, and well-structured representations that mitigate posterior collapse and improve geometric reconstruction. The DeepONet then exploits this compact latent encoding in its branch network, together with spatial coordinates in the trunk network, to predict temperature gradients efficiently and accurately. This hybrid approach not only enhances the quality of generated geometries and the accuracy of gradient prediction, but also provides a substantial advantage in inference efficiency compared to traditional numerical solvers. Overall, the study underscores the importance of structured latent representations for operator learning and highlights the potential of combining generative models and operator networks in thermal design and broader engineering applications.

Variational Rank Reduction Autoencoder

Deterministic Rank Reduction Autoencoders (RRAEs) enforce by construction a regularization on the latent space by applying a truncated SVD. While this regularization makes Autoencoders more powerful, using them for generative purposes is counter-intuitive due to their deterministic nature. On the other hand, Variational Autoencoders (VAEs) are well known for their generative abilities by learning a probabilistic latent space. In this paper, we present Variational Rank Reduction Autoencoders (VRRAEs), a model that leverages the advantages of both RRAEs and VAEs. Our claims and results show that when carefully sampling the latent space of RRAEs and further regularizing with the Kullback-Leibler (KL) divergence (similarly to VAEs), VRRAEs outperform RRAEs and VAEs. Additionally, we show that the regularization induced by the SVD not only makes VRRAEs better generators than VAEs, but also reduces the possibility of posterior collapse. Our results include a synthetic dataset of a small size that showcases the robustness of VRRAEs against collapse, and three real-world datasets; the MNIST, CelebA, and CIFAR-10, over which VRRAEs are shown to outperform both VAEs and RRAEs on many random generation and interpolation tasks based on the FID score.

A data-driven learned discretization approach in finite volume schemes for hyperbolic conservation laws and varying boundary conditions

This paper presents a data-driven finite volume method for solving 1D and 2D hyperbolic partial differential equations. This work builds upon the prior research incorporating a data-driven finite-difference approximation of smooth solutions of scalar conservation laws, where optimal coefficients of neural networks approximating space derivatives are learned based on accurate, but cumbersome solutions to these equations. We extend this approach to flux-limited finite volume schemes for hyperbolic scalar and systems of conservation laws. We also train the discretization to efficiently capture discontinuous solutions with shock and contact waves, as well as to the application of boundary conditions. The learning procedure of the data-driven model is extended through the definition of a new loss, paddings and adequate database. These new ingredients guarantee computational stability, preserve the accuracy of fine-grid solutions, and enhance overall performance. Numerical experiments using test cases from the literature in both one- and two-dimensional spaces demonstrate that the learned model accurately reproduces fine-grid results on very coarse meshes.

FFT-based surrogate modeling of auxetic metamaterials with real-time prediction of effective elastic properties and swift inverse design

Auxetic structures, known for their negative Poisson's ratio, exhibit effective elastic properties heavily influenced by their underlying structural geometry and base material properties. While periodic homogenization of auxetic unit cells can be used to investigate these properties, it is computationally expensive and limits design space exploration and inverse analysis. In this paper, surrogate models are developed for the real-time prediction of the effective elastic properties of auxetic unit cells with orthogonal voids of different shapes. The unit cells feature orthogonal voids in four distinct shapes, including rectangular, diamond, oval, and peanut-shaped voids, each characterized by specific void diameters. The generated surrogate models accept geometric parameters and the elastic properties of the base material as inputs to predict the effective elastic constants in real-time. This rapid evaluation enables a practical inverse analysis framework for obtaining the optimal design parameters that yield the desired effective response. The fast Fourier transform (FFT)-based homogenization approach is adopted to efficiently generate data for developing the surrogate models, bypassing concerns about periodic mesh generation and boundary conditions typically associated with the finite element method (FEM). The performance of the generated surrogate models is rigorously examined through a train/test split methodology, a parametric study, and an inverse problem. Finally, a graphical user interface (GUI) is developed, offering real-time prediction of the effective tangent stiffness and performing inverse analysis to determine optimal geometric parameters.

Rank Reduction Autoencoders -- Enhancing interpolation on nonlinear manifolds

The efficiency of classical Autoencoders (AEs) is limited in many practical situations. When the latent space is reduced through autoencoders, feature extraction becomes possible. However, overfitting is a common issue, leading to ``holes'' in AEs' interpolation capabilities. On the other hand, increasing the latent dimension results in a better approximation with fewer non-linearly coupled features (e.g., Koopman theory or kPCA), but it doesn't necessarily lead to dimensionality reduction, which makes feature extraction problematic. As a result, interpolating using Autoencoders gets harder. In this work, we introduce the Rank Reduction Autoencoder (RRAE), an autoencoder with an enlarged latent space, which is constrained to have a small pre-specified number of dominant singular values (i.e., low-rank). The latent space of RRAEs is large enough to enable accurate predictions while enabling feature extraction. As a result, the proposed autoencoder features a minimal rank linear latent space. To achieve what's proposed, two formulations are presented, a strong and a weak one, that build a reduced basis accurately representing the latent space. The first formulation consists of a truncated SVD in the latent space, while the second one adds a penalty term to the loss function. We show the efficiency of our formulations by using them for interpolation tasks and comparing the results to other autoencoders on both synthetic data and MNIST.

Graph neural networks informed locally by thermodynamics

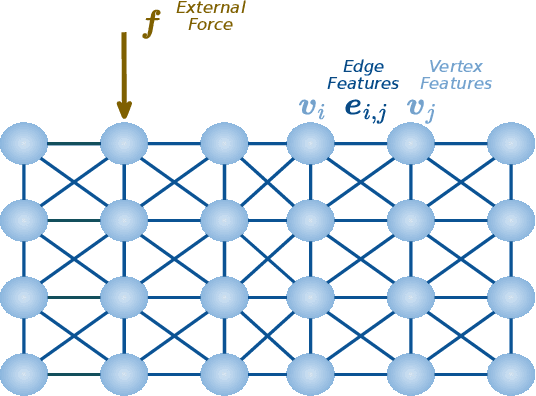
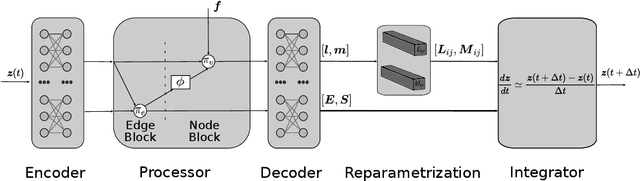
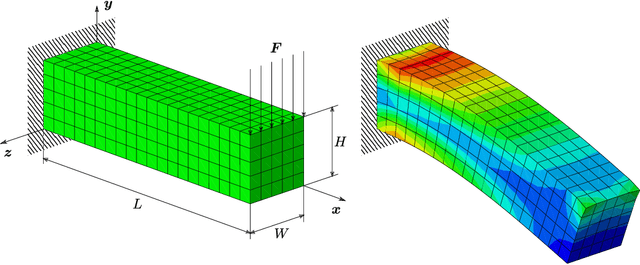
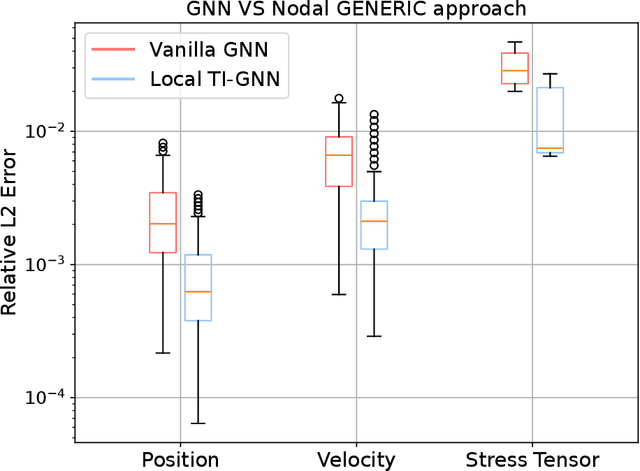
Thermodynamics-informed neural networks employ inductive biases for the enforcement of the first and second principles of thermodynamics. To construct these biases, a metriplectic evolution of the system is assumed. This provides excellent results, when compared to uninformed, black box networks. While the degree of accuracy can be increased in one or two orders of magnitude, in the case of graph networks, this requires assembling global Poisson and dissipation matrices, which breaks the local structure of such networks. In order to avoid this drawback, a local version of the metriplectic biases has been developed in this work, which avoids the aforementioned matrix assembly, thus preserving the node-by-node structure of the graph networks. We apply this framework for examples in the fields of solid and fluid mechanics. Our approach demonstrates significant computational efficiency and strong generalization capabilities, accurately making inferences on examples significantly different from those encountered during training.

A comparison of Single- and Double-generator formalisms for Thermodynamics-Informed Neural Networks

The development of inductive biases has been shown to be a very effective way to increase the accuracy and robustness of neural networks, particularly when they are used to predict physical phenomena. These biases significantly increase the certainty of predictions, decrease the error made and allow considerably smaller datasets to be used. There are a multitude of methods in the literature to develop these biases. One of the most effective ways, when dealing with physical phenomena, is to introduce physical principles of recognised validity into the network architecture. The problem becomes more complex without knowledge of the physical principles governing the phenomena under study. A very interesting possibility then is to turn to the principles of thermodynamics, which are universally valid, regardless of the level of abstraction of the description sought for the phenomenon under study. To ensure compliance with the principles of thermodynamics, there are formulations that have a long tradition in many branches of science. In the field of rheology, for example, two main types of formalisms are used to ensure compliance with these principles: one-generator and two-generator formalisms. In this paper we study the advantages and disadvantages of each, using classical problems with known solutions and synthetic data.

Thermodynamics-informed super-resolution of scarce temporal dynamics data

We present a method to increase the resolution of measurements of a physical system and subsequently predict its time evolution using thermodynamics-aware neural networks. Our method uses adversarial autoencoders, which reduce the dimensionality of the full order model to a set of latent variables that are enforced to match a prior, for example a normal distribution. Adversarial autoencoders are seen as generative models, and they can be trained to generate high-resolution samples from low-resoution inputs, meaning they can address the so-called super-resolution problem. Then, a second neural network is trained to learn the physical structure of the latent variables and predict their temporal evolution. This neural network is known as an structure-preserving neural network. It learns the metriplectic-structure of the system and applies a physical bias to ensure that the first and second principles of thermodynamics are fulfilled. The integrated trajectories are decoded to their original dimensionality, as well as to the higher dimensionality space produced by the adversarial autoencoder and they are compared to the ground truth solution. The method is tested with two examples of flow over a cylinder, where the fluid properties are varied between both examples.