Rank Reduction Autoencoders -- Enhancing interpolation on nonlinear manifolds

The efficiency of classical Autoencoders (AEs) is limited in many practical situations. When the latent space is reduced through autoencoders, feature extraction becomes possible. However, overfitting is a common issue, leading to ``holes'' in AEs' interpolation capabilities. On the other hand, increasing the latent dimension results in a better approximation with fewer non-linearly coupled features (e.g., Koopman theory or kPCA), but it doesn't necessarily lead to dimensionality reduction, which makes feature extraction problematic. As a result, interpolating using Autoencoders gets harder. In this work, we introduce the Rank Reduction Autoencoder (RRAE), an autoencoder with an enlarged latent space, which is constrained to have a small pre-specified number of dominant singular values (i.e., low-rank). The latent space of RRAEs is large enough to enable accurate predictions while enabling feature extraction. As a result, the proposed autoencoder features a minimal rank linear latent space. To achieve what's proposed, two formulations are presented, a strong and a weak one, that build a reduced basis accurately representing the latent space. The first formulation consists of a truncated SVD in the latent space, while the second one adds a penalty term to the loss function. We show the efficiency of our formulations by using them for interpolation tasks and comparing the results to other autoencoders on both synthetic data and MNIST.

Mesh sampling and weighting for the hyperreduction of nonlinear Petrov-Galerkin reduced-order models with local reduced-order bases

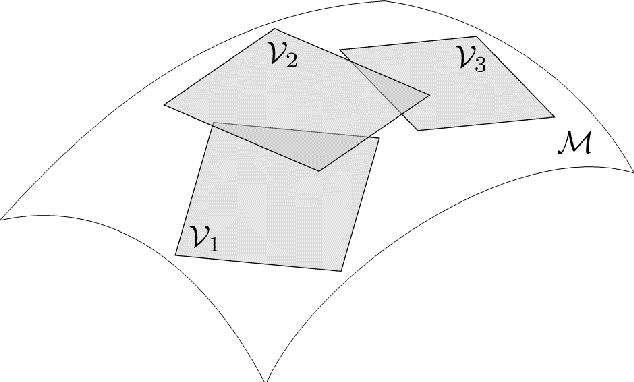
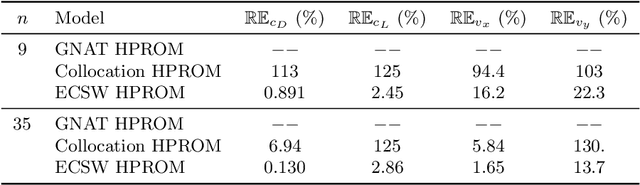
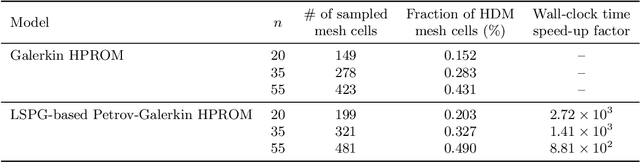
The energy-conserving sampling and weighting (ECSW) method is a hyperreduction method originally developed for accelerating the performance of Galerkin projection-based reduced-order models (PROMs) associated with large-scale finite element models, when the underlying projected operators need to be frequently recomputed as in parametric and/or nonlinear problems. In this paper, this hyperreduction method is extended to Petrov-Galerkin PROMs where the underlying high-dimensional models can be associated with arbitrary finite element, finite volume, and finite difference semi-discretization methods. Its scope is also extended to cover local PROMs based on piecewise-affine approximation subspaces, such as those designed for mitigating the Kolmogorov $n$-width barrier issue associated with convection-dominated flow problems. The resulting ECSW method is shown in this paper to be robust and accurate. In particular, its offline phase is shown to be fast and parallelizable, and the potential of its online phase for large-scale applications of industrial relevance is demonstrated for turbulent flow problems with $O(10^7)$ and $O(10^8)$ degrees of freedom. For such problems, the online part of the ECSW method proposed in this paper for Petrov-Galerkin PROMs is shown to enable wall-clock time and CPU time speedup factors of several orders of magnitude while delivering exceptional accuracy.

A computationally tractable framework for nonlinear dynamic multiscale modeling of membrane fabric

A general-purpose computational homogenization framework is proposed for the nonlinear dynamic analysis of membranes exhibiting complex microscale and/or mesoscale heterogeneity characterized by in-plane periodicity that cannot be effectively treated by a conventional method, such as woven fabrics. The proposed framework is a generalization of the ``Finite Element squared'' method in which a localized portion of the periodic subscale structure -- typically referred to as a Representative Volume Element (RVE) -- is modeled using finite elements. The numerical solution of displacement-driven problems using this model furnishes a mapping between the deformation gradient and the first Piola-Kirchhoff stress tensor. The approach involves the numerical enforcement of the plane stress constraint. Finally, computational tractability is achieved by introducing a regression-based surrogate model to avoid further solution of the RVE model when data sufficient to fit a model capable of delivering adequate approximations is available. For this purpose, a physics-inspired training regimen involving the utilization of our generalized FE$^2$ method to simulate a variety of numerical experiments -- including but not limited to uniaxial, biaxial and shear straining of a material coupon -- is proposed as a practical method for data collection. The proposed framework is demonstrated for a Mars landing application involving the supersonic inflation of an atmospheric aerodynamic decelerator system that includes a parachute canopy made of a woven fabric. Several alternative surrogate models are evaluated including a neural network.

On the stability of projection-based model order reduction for convection-dominated laminar and turbulent flows

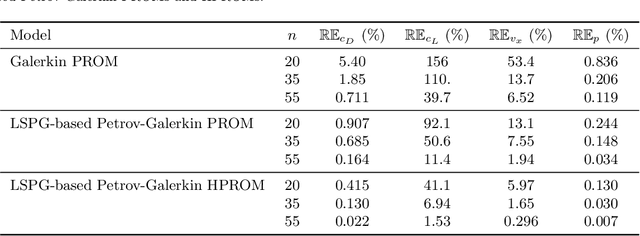
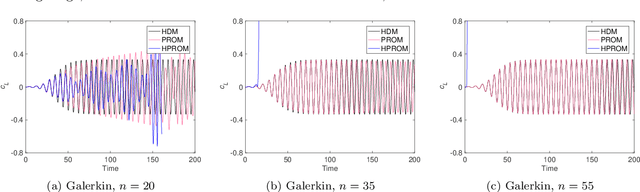
In the literature on projection-based nonlinear model order reduction for fluid dynamics problems, it is often claimed that due to modal truncation, a projection-based reduced-order model (PROM) does not resolve the dissipative regime of the turbulent energy cascade and therefore is numerically unstable. Efforts at addressing this claim have ranged from attempting to model the effects of the truncated modes to enriching the classical subspace of approximation in order to account for the truncated phenomena. This paper challenges this claim. Exploring the relationship between projection-based model order reduction and semi-discretization and using numerical evidence from three relevant flow problems, it argues in an orderly manner that the real culprit behind most if not all reported numerical instabilities of PROMs for turbulence and convection-dominated turbulent flow problems is the Galerkin framework that has been used for constructing the PROMs. The paper also shows that alternatively, a Petrov-Galerkin framework can be used to construct numerically stable PROMs for convection-dominated laminar as well as turbulent flow problems that are numerically stable and accurate, without resorting to additional closure models or tailoring of the subspace of approximation. It also shows that such alternative PROMs deliver significant speedup factors.

Neural Networks Predict Fluid Dynamics Solutions from Tiny Datasets

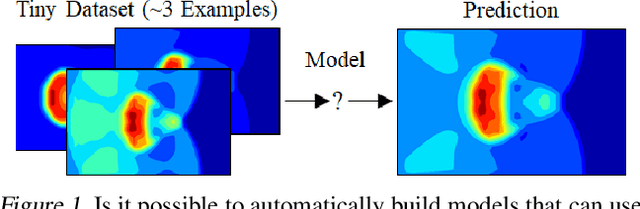
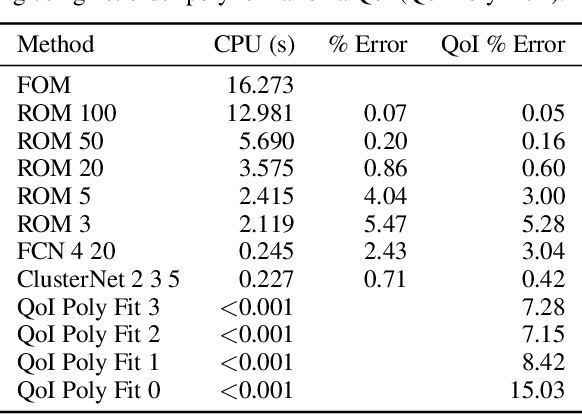
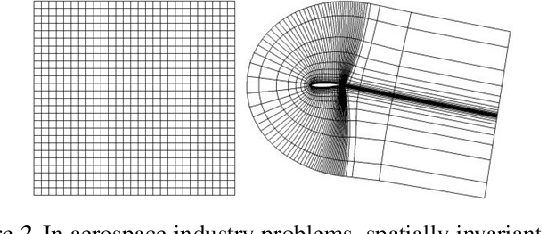
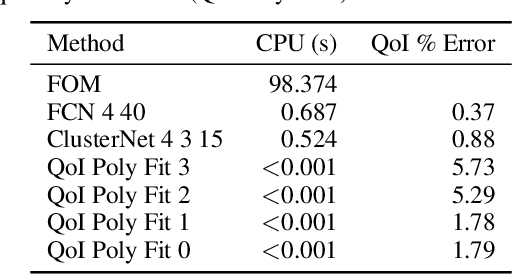
In computational fluid dynamics, it often takes days or weeks to simulate the aerodynamic behavior of designs such as jets, spacecraft, or gas turbine engines. One of the biggest open problems in the field is how to simulate such systems much more quickly with sufficient accuracy. Many approaches have been tried; some involve models of the underlying physics, while others are model-free and make predictions based only on existing simulation data. However, all previous approaches have severe shortcomings or limitations. We present a novel approach: we reformulate the prediction problem to effectively increase the size of the otherwise tiny datasets, and we introduce a new neural network architecture (called a cluster network) with an inductive bias well-suited to fluid dynamics problems. Compared to state-of-the-art model-based approximations, we show that our approach is nearly as accurate, an order of magnitude faster and vastly easier to apply. Moreover, our method outperforms previous model-free approaches.