Noah Youkilis
On the stability of projection-based model order reduction for convection-dominated laminar and turbulent flows
Jan 27, 2020
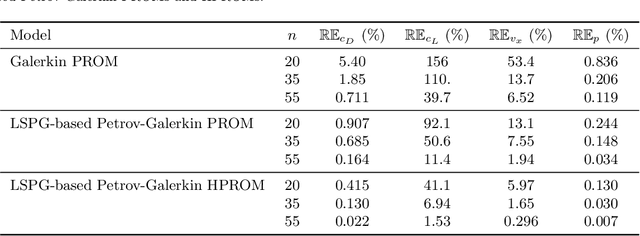
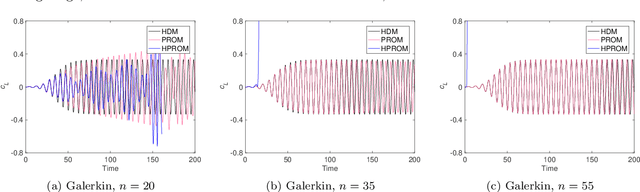
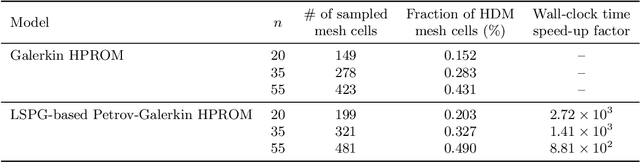
Abstract:In the literature on projection-based nonlinear model order reduction for fluid dynamics problems, it is often claimed that due to modal truncation, a projection-based reduced-order model (PROM) does not resolve the dissipative regime of the turbulent energy cascade and therefore is numerically unstable. Efforts at addressing this claim have ranged from attempting to model the effects of the truncated modes to enriching the classical subspace of approximation in order to account for the truncated phenomena. This paper challenges this claim. Exploring the relationship between projection-based model order reduction and semi-discretization and using numerical evidence from three relevant flow problems, it argues in an orderly manner that the real culprit behind most if not all reported numerical instabilities of PROMs for turbulence and convection-dominated turbulent flow problems is the Galerkin framework that has been used for constructing the PROMs. The paper also shows that alternatively, a Petrov-Galerkin framework can be used to construct numerically stable PROMs for convection-dominated laminar as well as turbulent flow problems that are numerically stable and accurate, without resorting to additional closure models or tailoring of the subspace of approximation. It also shows that such alternative PROMs deliver significant speedup factors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge