Mesh sampling and weighting for the hyperreduction of nonlinear Petrov-Galerkin reduced-order models with local reduced-order bases
Paper and Code
Aug 06, 2020

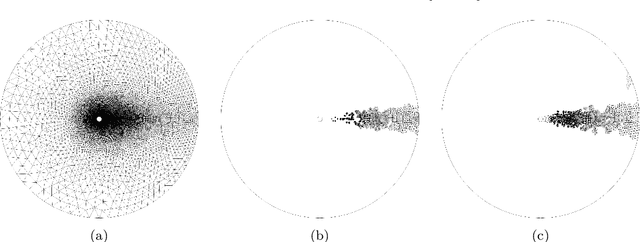
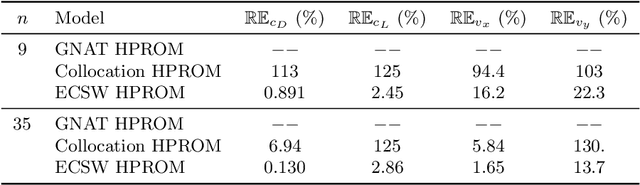
The energy-conserving sampling and weighting (ECSW) method is a hyperreduction method originally developed for accelerating the performance of Galerkin projection-based reduced-order models (PROMs) associated with large-scale finite element models, when the underlying projected operators need to be frequently recomputed as in parametric and/or nonlinear problems. In this paper, this hyperreduction method is extended to Petrov-Galerkin PROMs where the underlying high-dimensional models can be associated with arbitrary finite element, finite volume, and finite difference semi-discretization methods. Its scope is also extended to cover local PROMs based on piecewise-affine approximation subspaces, such as those designed for mitigating the Kolmogorov $n$-width barrier issue associated with convection-dominated flow problems. The resulting ECSW method is shown in this paper to be robust and accurate. In particular, its offline phase is shown to be fast and parallelizable, and the potential of its online phase for large-scale applications of industrial relevance is demonstrated for turbulent flow problems with $O(10^7)$ and $O(10^8)$ degrees of freedom. For such problems, the online part of the ECSW method proposed in this paper for Petrov-Galerkin PROMs is shown to enable wall-clock time and CPU time speedup factors of several orders of magnitude while delivering exceptional accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge