Graph neural networks informed locally by thermodynamics

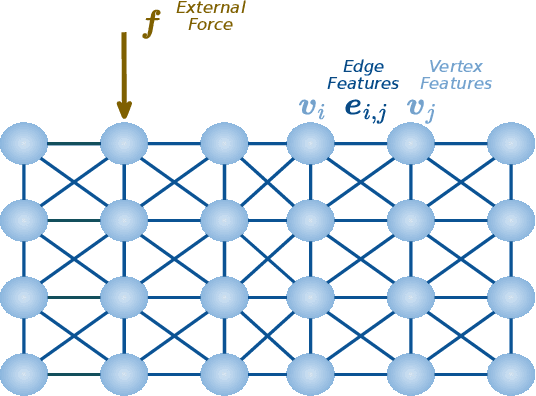
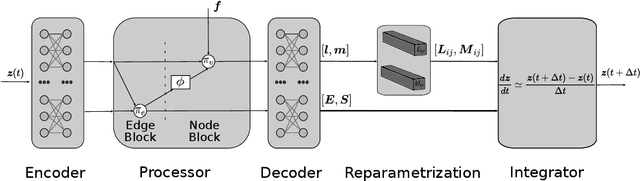
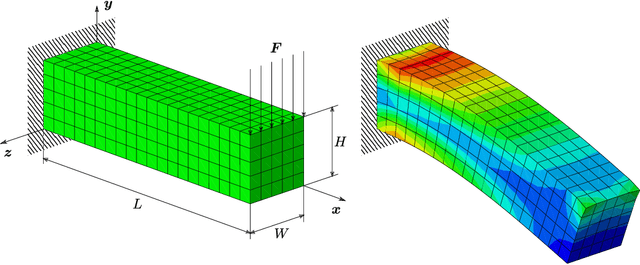
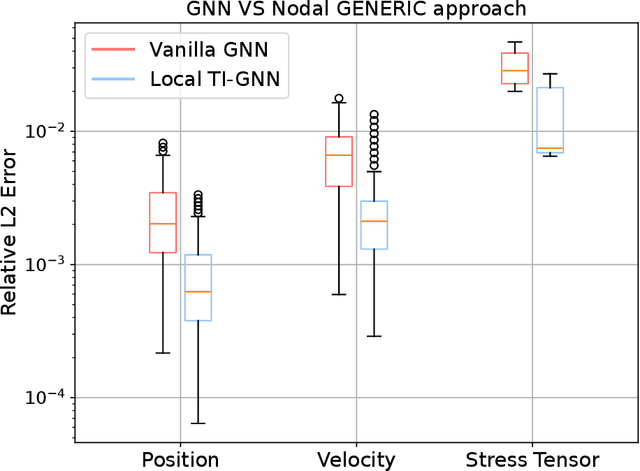
Thermodynamics-informed neural networks employ inductive biases for the enforcement of the first and second principles of thermodynamics. To construct these biases, a metriplectic evolution of the system is assumed. This provides excellent results, when compared to uninformed, black box networks. While the degree of accuracy can be increased in one or two orders of magnitude, in the case of graph networks, this requires assembling global Poisson and dissipation matrices, which breaks the local structure of such networks. In order to avoid this drawback, a local version of the metriplectic biases has been developed in this work, which avoids the aforementioned matrix assembly, thus preserving the node-by-node structure of the graph networks. We apply this framework for examples in the fields of solid and fluid mechanics. Our approach demonstrates significant computational efficiency and strong generalization capabilities, accurately making inferences on examples significantly different from those encountered during training.

A comparison of Single- and Double-generator formalisms for Thermodynamics-Informed Neural Networks

The development of inductive biases has been shown to be a very effective way to increase the accuracy and robustness of neural networks, particularly when they are used to predict physical phenomena. These biases significantly increase the certainty of predictions, decrease the error made and allow considerably smaller datasets to be used. There are a multitude of methods in the literature to develop these biases. One of the most effective ways, when dealing with physical phenomena, is to introduce physical principles of recognised validity into the network architecture. The problem becomes more complex without knowledge of the physical principles governing the phenomena under study. A very interesting possibility then is to turn to the principles of thermodynamics, which are universally valid, regardless of the level of abstraction of the description sought for the phenomenon under study. To ensure compliance with the principles of thermodynamics, there are formulations that have a long tradition in many branches of science. In the field of rheology, for example, two main types of formalisms are used to ensure compliance with these principles: one-generator and two-generator formalisms. In this paper we study the advantages and disadvantages of each, using classical problems with known solutions and synthetic data.

Thermodynamics-informed super-resolution of scarce temporal dynamics data

We present a method to increase the resolution of measurements of a physical system and subsequently predict its time evolution using thermodynamics-aware neural networks. Our method uses adversarial autoencoders, which reduce the dimensionality of the full order model to a set of latent variables that are enforced to match a prior, for example a normal distribution. Adversarial autoencoders are seen as generative models, and they can be trained to generate high-resolution samples from low-resoution inputs, meaning they can address the so-called super-resolution problem. Then, a second neural network is trained to learn the physical structure of the latent variables and predict their temporal evolution. This neural network is known as an structure-preserving neural network. It learns the metriplectic-structure of the system and applies a physical bias to ensure that the first and second principles of thermodynamics are fulfilled. The integrated trajectories are decoded to their original dimensionality, as well as to the higher dimensionality space produced by the adversarial autoencoder and they are compared to the ground truth solution. The method is tested with two examples of flow over a cylinder, where the fluid properties are varied between both examples.

Port-metriplectic neural networks: thermodynamics-informed machine learning of complex physical systems

We develop inductive biases for the machine learning of complex physical systems based on the port-Hamiltonian formalism. To satisfy by construction the principles of thermodynamics in the learned physics (conservation of energy, non-negative entropy production), we modify accordingly the port-Hamiltonian formalism so as to achieve a port-metriplectic one. We show that the constructed networks are able to learn the physics of complex systems by parts, thus alleviating the burden associated to the experimental characterization and posterior learning process of this kind of systems. Predictions can be done, however, at the scale of the complete system. Examples are shown on the performance of the proposed technique.

Thermodynamics-informed neural networks for physically realistic mixed reality

The imminent impact of immersive technologies in society urges for active research in real-time and interactive physics simulation for virtual worlds to be realistic. In this context, realistic means to be compliant to the laws of physics. In this paper we present a method for computing the dynamic response of (possibly non-linear and dissipative) deformable objects induced by real-time user interactions in mixed reality using deep learning. The graph-based architecture of the method ensures the thermodynamic consistency of the predictions, whereas the visualization pipeline allows a natural and realistic user experience. Two examples of virtual solids interacting with virtual or physical solids in mixed reality scenarios are provided to prove the performance of the method.

Thermodynamics-informed graph neural networks

In this paper we present a deep learning method to predict the time evolution of dissipative dynamical systems. We propose using both geometric and thermodynamic inductive biases to improve accuracy and generalization of the resulting integration scheme. The first is achieved with Graph Neural Networks, which induces a non-Euclidean geometrical prior and permutation invariant node and edge update functions. The second bias is forced by learning the GENERIC structure of the problem, an extension of the Hamiltonian formalism, to model more general non-conservative dynamics. Several examples are provided in both Eulerian and Lagrangian description in the context of fluid and solid mechanics respectively.