Graph neural networks informed locally by thermodynamics

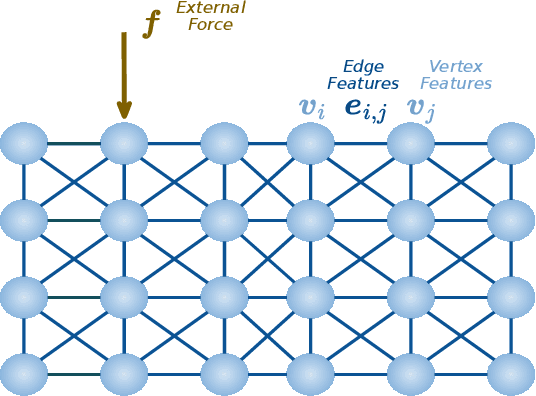
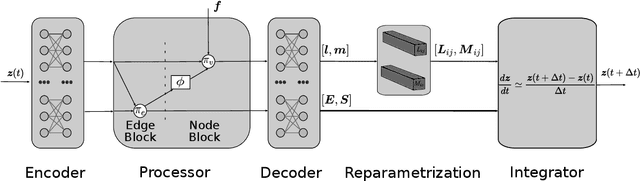
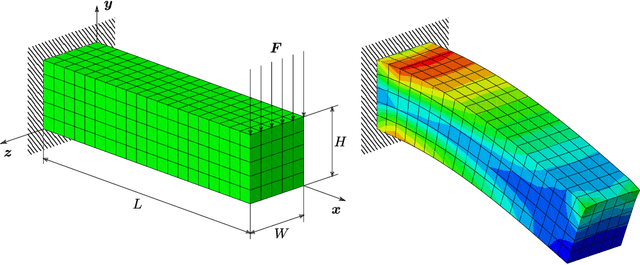
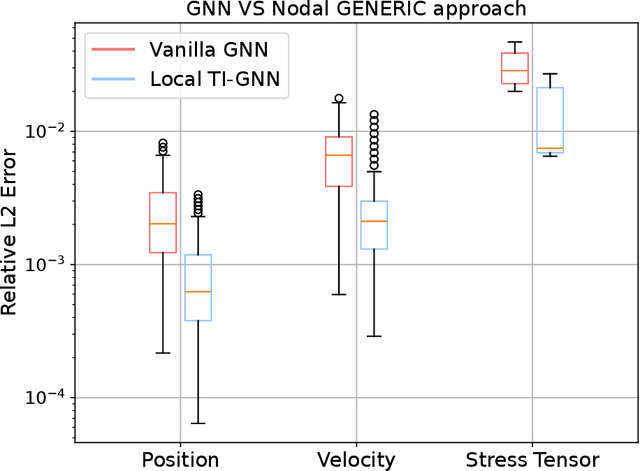
Thermodynamics-informed neural networks employ inductive biases for the enforcement of the first and second principles of thermodynamics. To construct these biases, a metriplectic evolution of the system is assumed. This provides excellent results, when compared to uninformed, black box networks. While the degree of accuracy can be increased in one or two orders of magnitude, in the case of graph networks, this requires assembling global Poisson and dissipation matrices, which breaks the local structure of such networks. In order to avoid this drawback, a local version of the metriplectic biases has been developed in this work, which avoids the aforementioned matrix assembly, thus preserving the node-by-node structure of the graph networks. We apply this framework for examples in the fields of solid and fluid mechanics. Our approach demonstrates significant computational efficiency and strong generalization capabilities, accurately making inferences on examples significantly different from those encountered during training.

MORPH-DSLAM: Model Order Reduction for PHysics-based Deformable SLAM

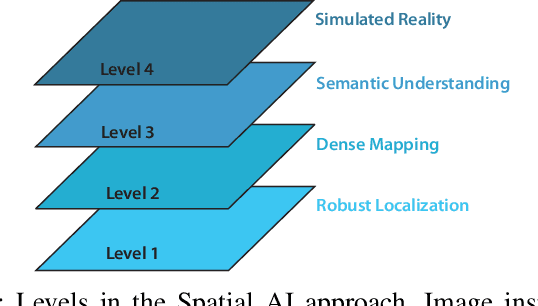
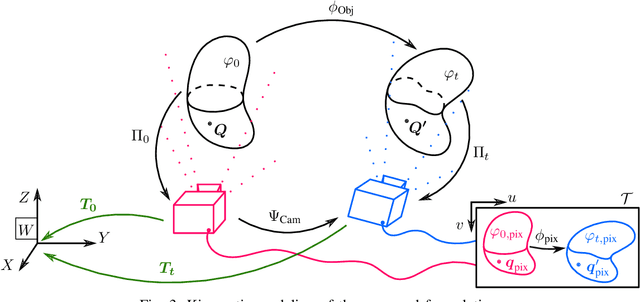
We propose a new methodology to estimate the 3D displacement field of deformable objects from video sequences using standard monocular cameras. We solve in real time the complete (possibly visco-)hyperelasticity problem to properly describe the strain and stress fields that are consistent with the displacements captured by the images, constrained by real physics. We do not impose any ad-hoc prior or energy minimization in the external surface, since the real and complete mechanics problem is solved. This means that we can also estimate the internal state of the objects, even in occluded areas, just by observing the external surface and the knowledge of material properties and geometry. Solving this problem in real time using a realistic constitutive law, usually non-linear, is out of reach for current systems. To overcome this difficulty, we solve off-line a parametrized problem that considers each source of variability in the problem as a new parameter and, consequently, as a new dimension in the formulation. Model Order Reduction methods allow us to reduce the dimensionality of the problem, and therefore, its computational cost, while preserving the visualization of the solution in the high-dimensionality space. This allows an accurate estimation of the object deformations, improving also the robustness in the 3D points estimation.