Thermodynamics of learning physical phenomena

Thermodynamics could be seen as an expression of physics at a high epistemic level. As such, its potential as an inductive bias to help machine learning procedures attain accurate and credible predictions has been recently realized in many fields. We review how thermodynamics provides helpful insights in the learning process. At the same time, we study the influence of aspects such as the scale at which a given phenomenon is to be described, the choice of relevant variables for this description or the different techniques available for the learning process.

Physics-informed Reinforcement Learning for Perception and Reasoning about Fluids

Learning and reasoning about physical phenomena is still a challenge in robotics development, and computational sciences play a capital role in the search for accurate methods able to provide explanations for past events and rigorous forecasts of future situations. We propose a physics-informed reinforcement learning strategy for fluid perception and reasoning from observations. As a model problem, we take the sloshing phenomena of different fluids contained in a glass. Starting from full-field and high-resolution synthetic data for a particular fluid, we develop a method for the tracking (perception) and analysis (reasoning) of any previously unseen liquid whose free surface is observed with a commodity camera. This approach demonstrates the importance of physics and knowledge not only in data-driven (grey box) modeling but also in the correction for real physics adaptation in low data regimes and partial observations of the dynamics. The method here presented is extensible to other domains such as the development of cognitive digital twins, able to learn from observation of phenomena for which they have not been trained explicitly.

Monitoring weeder robots and anticipating their functioning by using advanced topological data analysis

The present paper aims at analyzing the topological content of the complex trajectories that weeder-autonomous robots follow in operation. We will prove that the topological descriptors of these trajectories are affected by the robot environment as well as by the robot state, with respect to maintenance operations. Topological Data Analysis will be used for extracting the trajectory descriptors, based on homology persistence. Then, appropriate metrics will be applied in order to compare that topological representation of the trajectories, for classifying them or for making efficient pattern recognition.

Physics perception in sloshing scenes with guaranteed thermodynamic consistency

Physics perception very often faces the problem that only limited data or partial measurements on the scene are available. In this work, we propose a strategy to learn the full state of sloshing liquids from measurements of the free surface. Our approach is based on recurrent neural networks (RNN) that project the limited information available to a reduced-order manifold so as to not only reconstruct the unknown information, but also to be capable of performing fluid reasoning about future scenarios in real time. To obtain physically consistent predictions, we train deep neural networks on the reduced-order manifold that, through the employ of inductive biases, ensure the fulfillment of the principles of thermodynamics. RNNs learn from history the required hidden information to correlate the limited information with the latent space where the simulation occurs. Finally, a decoder returns data back to the high-dimensional manifold, so as to provide the user with insightful information in the form of augmented reality. This algorithm is connected to a computer vision system to test the performance of the proposed methodology with real information, resulting in a system capable of understanding and predicting future states of the observed fluid in real-time.

Learning stable reduced-order models for hybrid twins

The concept of Hybrid Twin (HT) has recently received a growing interest thanks to the availability of powerful machine learning techniques. This twin concept combines physics-based models within a model-order reduction framework-to obtain real-time feedback rates-and data science. Thus, the main idea of the HT is to develop on-the-fly data-driven models to correct possible deviations between measurements and physics-based model predictions. This paper is focused on the computation of stable, fast and accurate corrections in the Hybrid Twin framework. Furthermore, regarding the delicate and important problem of stability, a new approach is proposed, introducing several sub-variants and guaranteeing a low computational cost as well as the achievement of a stable time-integration.

MORPH-DSLAM: Model Order Reduction for PHysics-based Deformable SLAM

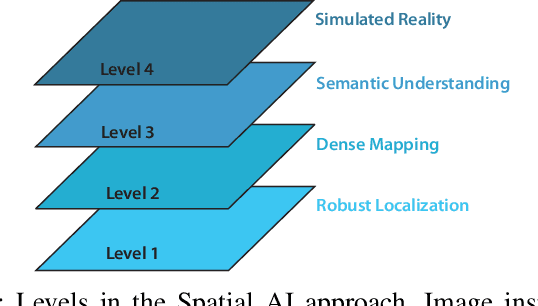
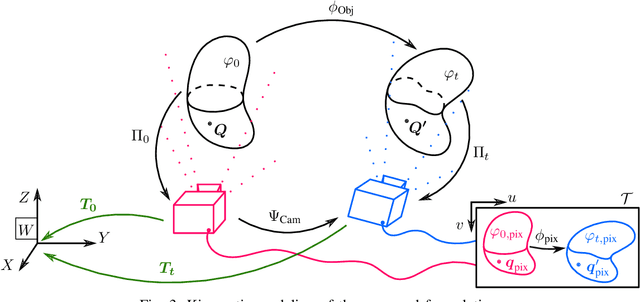
We propose a new methodology to estimate the 3D displacement field of deformable objects from video sequences using standard monocular cameras. We solve in real time the complete (possibly visco-)hyperelasticity problem to properly describe the strain and stress fields that are consistent with the displacements captured by the images, constrained by real physics. We do not impose any ad-hoc prior or energy minimization in the external surface, since the real and complete mechanics problem is solved. This means that we can also estimate the internal state of the objects, even in occluded areas, just by observing the external surface and the knowledge of material properties and geometry. Solving this problem in real time using a realistic constitutive law, usually non-linear, is out of reach for current systems. To overcome this difficulty, we solve off-line a parametrized problem that considers each source of variability in the problem as a new parameter and, consequently, as a new dimension in the formulation. Model Order Reduction methods allow us to reduce the dimensionality of the problem, and therefore, its computational cost, while preserving the visualization of the solution in the high-dimensionality space. This allows an accurate estimation of the object deformations, improving also the robustness in the 3D points estimation.

Deep learning of thermodynamics-aware reduced-order models from data

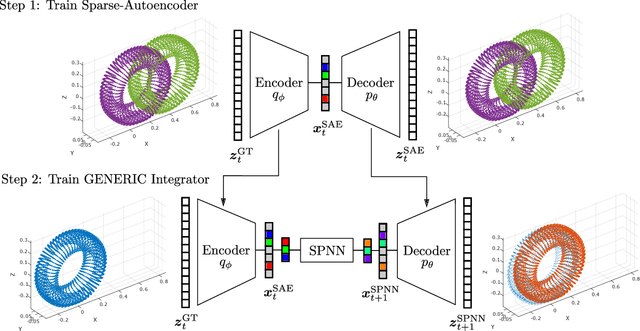
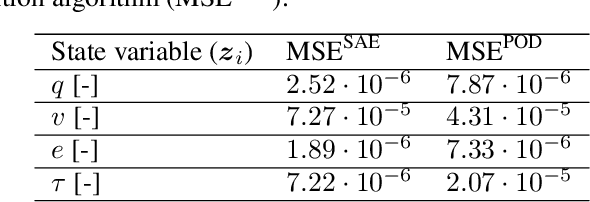
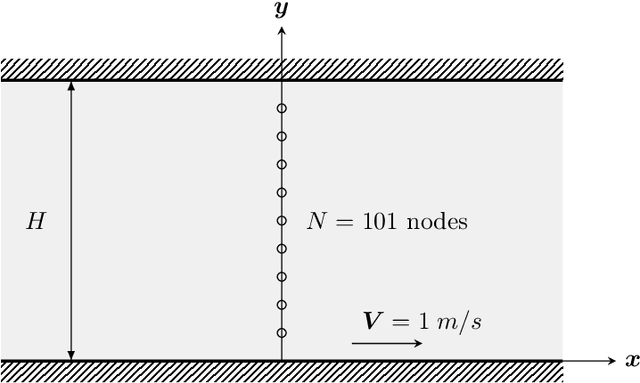
We present an algorithm to learn the relevant latent variables of a large-scale discretized physical system and predict its time evolution using thermodynamically-consistent deep neural networks. Our method relies on sparse autoencoders, which reduce the dimensionality of the full order model to a set of sparse latent variables with no prior knowledge of the coded space dimensionality. Then, a second neural network is trained to learn the metriplectic structure of those reduced physical variables and predict its time evolution with a so-called structure-preserving neural network. This data-based integrator is guaranteed to conserve the total energy of the system and the entropy inequality, and can be applied to both conservative and dissipative systems. The integrated paths can then be decoded to the original full-dimensional manifold and be compared to the ground truth solution. This method is tested with two examples applied to fluid and solid mechanics.

Structure-preserving neural networks

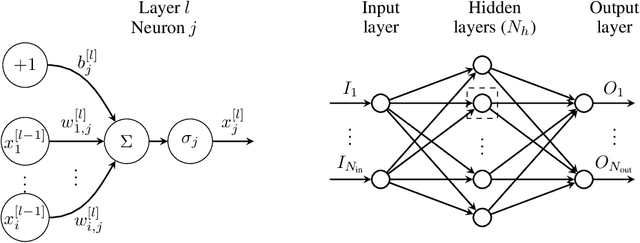
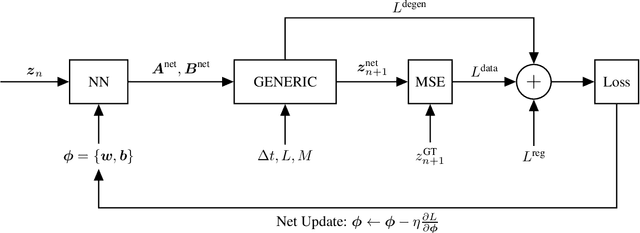
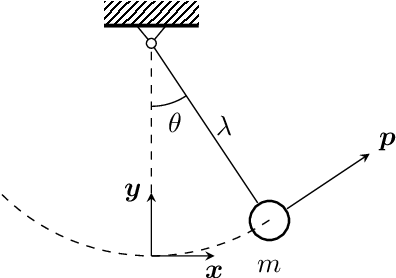
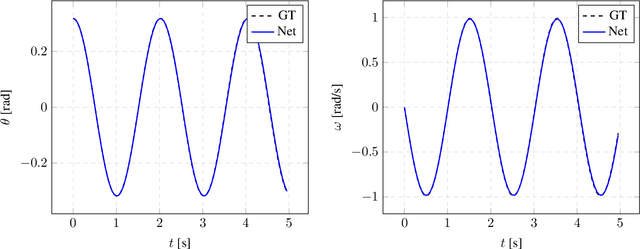
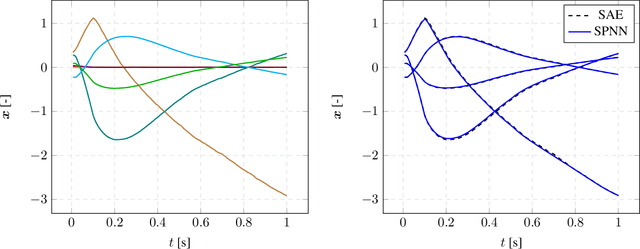
We develop a method to learn physical systems from data that employs feedforward neural networks and whose predictions comply with the first and second principles of thermodynamics. The method employs a minimum amount of data by enforcing the metriplectic structure of dissipative Hamiltonian systems in the form of the so-called General Equation for the Non-Equilibrium Reversible-Irreversible Coupling, GENERIC [M. Grmela and H.C Oettinger (1997). Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E. 56 (6): 6620-6632]. The method does not need to enforce any kind of balance equation, and thus no previous knowledge on the nature of the system is needed. Conservation of energy and dissipation of entropy in the prediction of previously unseen situations arise as a natural by-product of the structure of the method. Examples of the performance of the method are shown that include conservative as well as dissipative systems, discrete as well as continuous ones.