Data-driven particle dynamics: Structure-preserving coarse-graining for emergent behavior in non-equilibrium systems

Multiscale systems are ubiquitous in science and technology, but are notoriously challenging to simulate as short spatiotemporal scales must be appropriately linked to emergent bulk physics. When expensive high-dimensional dynamical systems are coarse-grained into low-dimensional models, the entropic loss of information leads to emergent physics which are dissipative, history-dependent, and stochastic. To machine learn coarse-grained dynamics from time-series observations of particle trajectories, we propose a framework using the metriplectic bracket formalism that preserves these properties by construction; most notably, the framework guarantees discrete notions of the first and second laws of thermodynamics, conservation of momentum, and a discrete fluctuation-dissipation balance crucial for capturing non-equilibrium statistics. We introduce the mathematical framework abstractly before specializing to a particle discretization. As labels are generally unavailable for entropic state variables, we introduce a novel self-supervised learning strategy to identify emergent structural variables. We validate the method on benchmark systems and demonstrate its utility on two challenging examples: (1) coarse-graining star polymers at challenging levels of coarse-graining while preserving non-equilibrium statistics, and (2) learning models from high-speed video of colloidal suspensions that capture coupling between local rearrangement events and emergent stochastic dynamics. We provide open-source implementations in both PyTorch and LAMMPS, enabling large-scale inference and extensibility to diverse particle-based systems.

Deep learning of thermodynamics-aware reduced-order models from data

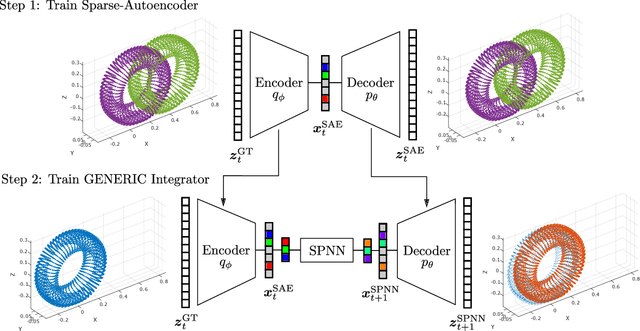
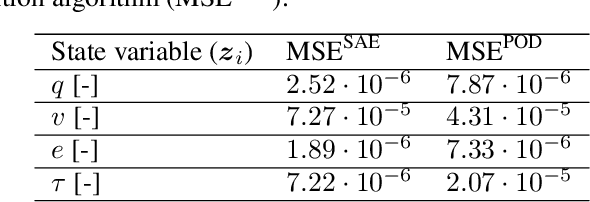
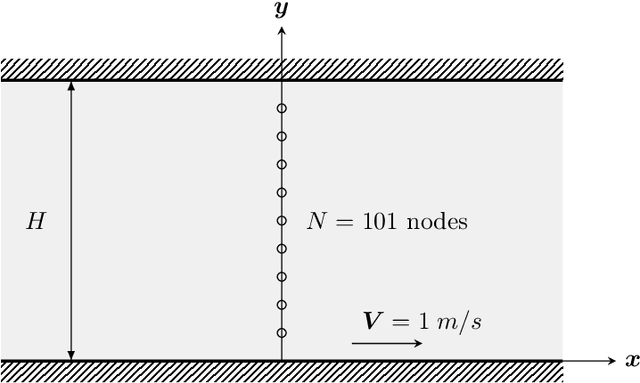
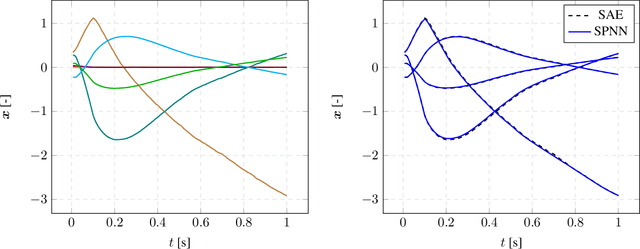
We present an algorithm to learn the relevant latent variables of a large-scale discretized physical system and predict its time evolution using thermodynamically-consistent deep neural networks. Our method relies on sparse autoencoders, which reduce the dimensionality of the full order model to a set of sparse latent variables with no prior knowledge of the coded space dimensionality. Then, a second neural network is trained to learn the metriplectic structure of those reduced physical variables and predict its time evolution with a so-called structure-preserving neural network. This data-based integrator is guaranteed to conserve the total energy of the system and the entropy inequality, and can be applied to both conservative and dissipative systems. The integrated paths can then be decoded to the original full-dimensional manifold and be compared to the ground truth solution. This method is tested with two examples applied to fluid and solid mechanics.

Structure-preserving neural networks

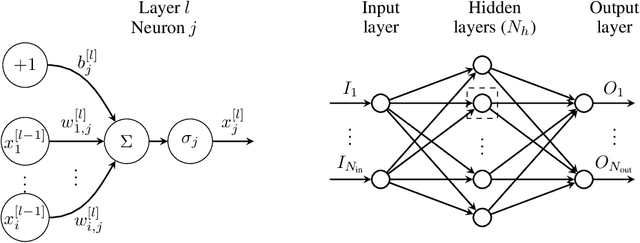
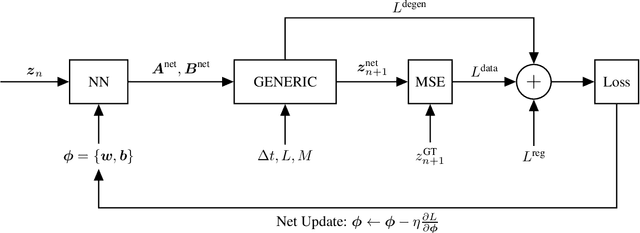
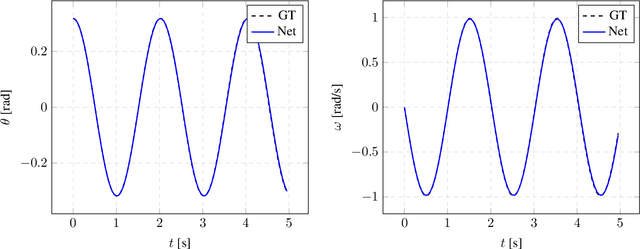
We develop a method to learn physical systems from data that employs feedforward neural networks and whose predictions comply with the first and second principles of thermodynamics. The method employs a minimum amount of data by enforcing the metriplectic structure of dissipative Hamiltonian systems in the form of the so-called General Equation for the Non-Equilibrium Reversible-Irreversible Coupling, GENERIC [M. Grmela and H.C Oettinger (1997). Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E. 56 (6): 6620-6632]. The method does not need to enforce any kind of balance equation, and thus no previous knowledge on the nature of the system is needed. Conservation of energy and dissipation of entropy in the prediction of previously unseen situations arise as a natural by-product of the structure of the method. Examples of the performance of the method are shown that include conservative as well as dissipative systems, discrete as well as continuous ones.

A Computational Model of a Single-Photon Avalanche Diode Sensor for Transient Imaging

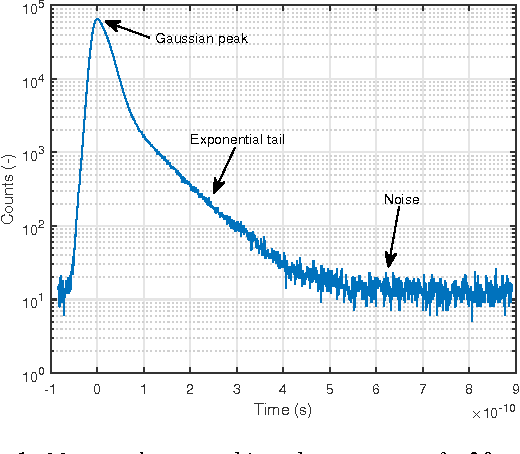
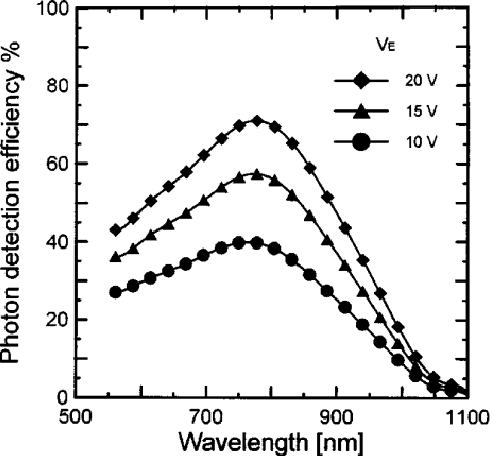
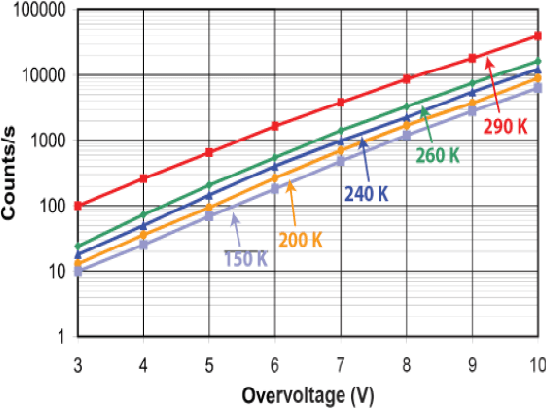
Single-Photon Avalanche Diodes (SPAD) are affordable photodetectors, capable to collect extremely fast low-energy events, due to their single-photon sensibility. This makes them very suitable for time-of-flight-based range imaging systems, allowing to reduce costs and power requirements, without sacrifizing much temporal resolution. In this work we describe a computational model to simulate the behaviour of SPAD sensors, aiming to provide a realistic camera model for time-resolved light transport simulation, with applications on prototyping new reconstructions techniques based on SPAD time-of-flight data. Our model accounts for the major effects of the sensor on the incoming signal. We compare our model against real-world measurements, and apply it to a variety of scenarios, including complex multiply-scattered light transport.