Wasserstein Distributionally Robust Bayesian Optimization with Continuous Context

We address the challenge of sequential data-driven decision-making under context distributional uncertainty. This problem arises in numerous real-world scenarios where the learner optimizes black-box objective functions in the presence of uncontrollable contextual variables. We consider the setting where the context distribution is uncertain but known to lie within an ambiguity set defined as a ball in the Wasserstein distance. We propose a novel algorithm for Wasserstein Distributionally Robust Bayesian Optimization that can handle continuous context distributions while maintaining computational tractability. Our theoretical analysis combines recent results in self-normalized concentration in Hilbert spaces and finite-sample bounds for distributionally robust optimization to establish sublinear regret bounds that match state-of-the-art results. Through extensive comparisons with existing approaches on both synthetic and real-world problems, we demonstrate the simplicity, effectiveness, and practical applicability of our proposed method.

Stochastic MPC for energy hubs using data driven demand forecasting

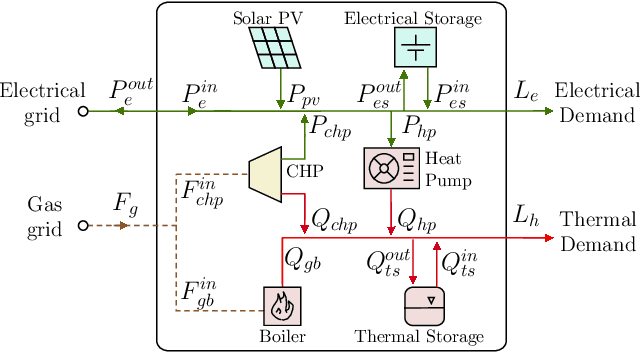
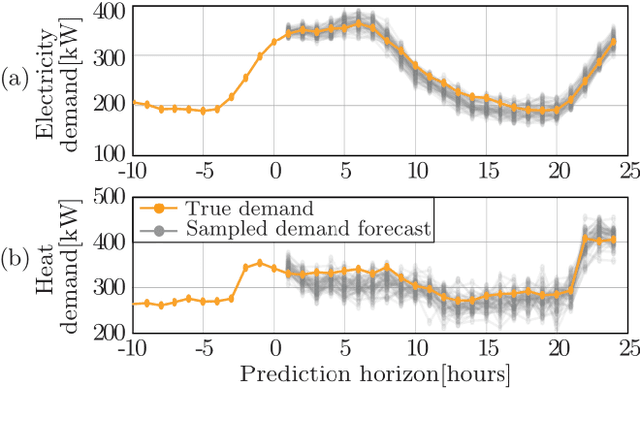
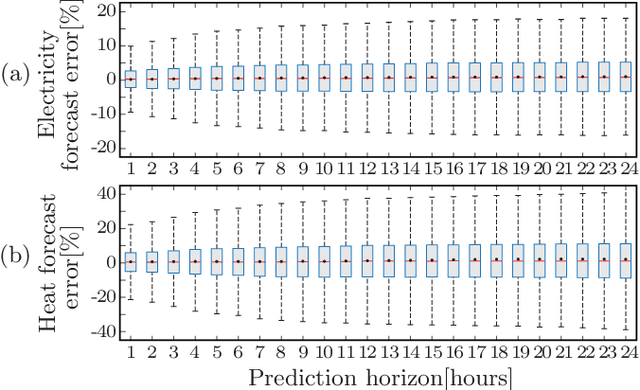
Energy hubs convert and distribute energy resources by combining different energy inputs through multiple conversion and storage components. The optimal operation of the energy hub exploits its flexibility to increase the energy efficiency and reduce the operational costs. However, uncertainties in the demand present challenges to energy hub optimization. In this paper, we propose a stochastic MPC controller to minimize energy costs using chance constraints for the uncertain electricity and thermal demands. Historical data is used to build a demand prediction model based on Gaussian processes to generate a forecast of the future electricity and heat demands. The stochastic optimization problem is solved via the Scenario Approach by sampling multi-step demand trajectories from the derived prediction model. The performance of the proposed predictor and of the stochastic controller is verified on a simulated energy hub model and demand data from a real building.

NMPC trajectory planner for urban autonomous driving

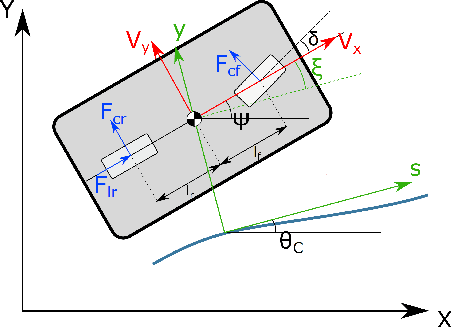
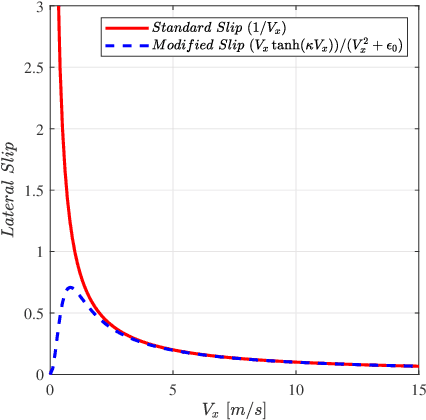
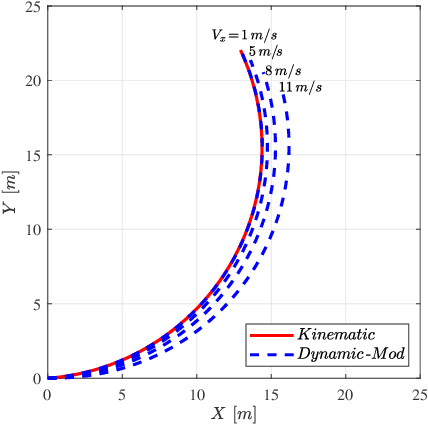
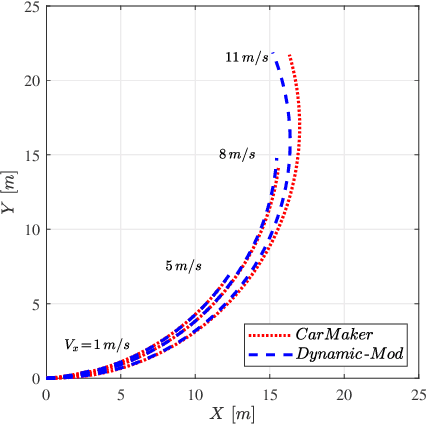
This paper presents a trajectory planner for autonomous driving based on a Nonlinear Model Predictive Control (NMPC) algorithm that accounts for Pacejka's nonlinear lateral tyre dynamics as well as for zero speed conditions through a novel slip angles calculation. In the NMPC framework, road boundaries and obstacles (both static and moving) are taken into account thanks to soft and hard constraints implementation. The numerical solution of the NMPC problem is carried out using ACADO toolkit coupled with the quadratic programming solver qpOASES. The effectiveness of the proposed NMPC trajectory planner has been tested using CarMaker multibody models. Time analysis results provided by the simulations shown, state that the proposed algorithm can be implemented on the real-time control framework of an autonomous vehicle under the assumption of data coming from an upstream estimation block.