Flow-Corrected Shape Optimization: Taming Manifold Drift in High-Dimensional 3D Models

Optimizing 3D shapes within the latent spaces of deep generative models is fundamental to computer assisted engineering, yet remains prone to a critical failure mode we term manifold drift: the tendency of gradient-based optimization to move latent vectors away from the manifold of valid shapes. This problem is exacerbated in state-of-the-art 3D shape generative models that operate in increasingly high-dimensional latent spaces where valid shapes occupy a vanishingly small fraction of the full space. Existing mitigation strategies, including latent regularization and flow-matching approaches, either sacrifice expressiveness, demand a difficult trade-off between objective guidance and generative fidelity that remains prone to manifold drift, or are computationally infeasible to scale to modern, large-capacity 3D shape models. We introduce a novel optimizer-corrector framework that alternates between gradient steps for objective minimization and guided flow matching to drive the latent state back to the valid shape manifold. By decoupling objective minimization from flow-based correction, optimizing freely and correcting strictly, this alternating design avoids inherent trade-offs, preserving geometric validity without sacrificing expressiveness while remaining computationally feasible on modern 3D shape models. We demonstrate its effectiveness across generative priors of varying complexity, from simple vector latent spaces to large-scale architectures across a variety of downstream optimization tasks, including aerodynamic drag reduction and object compliance optimization.

S2MDF: A Plug-And-Play Layer for Intersection-Free Multi-Object Signed Distance Fields

Compositional implicit surface representations model scenes as collections of objects, each encoded by a Signed Distance Field (SDF). A fundamental limitation of this approach is that multiple SDFs can produce geometries that interpenetrate, violating physical plausibility. Existing mitigation strategies rely on soft penalty terms that reduce but do not eliminate intersections, and require careful loss weighting. To truly prevent interpenetration, we propose a hard constraint on vector-valued SDFs and introduce S2MDF, a lightweight plug-and-play module that enforces the constraint on any object-compositional SDF representation without architectural modifications. It introduces negligible computational overhead and is compatible with linearly-interpolated standard meshing algorithms such as Marching Cubes. It can be applied during training or as a post-processing step. Experiments on multiple state-of-the-art compositional methods show that S2MDF reduces intersections to numerical precision while preserving reconstruction quality, outperforming existing mitigation strategies.

Gradient Distance Function

Unsigned Distance Functions (UDFs) can be used to represent non-watertight surfaces in a deep learning framework. However, UDFs tend to be brittle and difficult to learn, in part because the surface is located exactly where the UDF is non-differentiable. In this work, we show that Gradient Distance Functions (GDFs) can remedy this by being differentiable at the surface while still being able to represent open surfaces. This is done by associating to each 3D point a 3D vector whose norm is taken to be the unsigned distance to the surface and whose orientation is taken to be the direction towards the closest surface point. We demonstrate the effectiveness of GDFs on ShapeNet Car, Multi-Garment, and 3D-Scene datasets with both single-shape reconstruction networks or categorical auto-decoders.

Neural Surface Detection for Unsigned Distance Fields

Extracting surfaces from Signed Distance Fields (SDFs) can be accomplished using traditional algorithms, such as Marching Cubes. However, since they rely on sign flips across the surface, these algorithms cannot be used directly on Unsigned Distance Fields (UDFs). In this work, we introduce a deep-learning approach to taking a UDF and turning it locally into an SDF, so that it can be effectively triangulated using existing algorithms. We show that it achieves better accuracy in surface detection than existing methods. Furthermore it generalizes well to unseen shapes and datasets, while being parallelizable. We also demonstrate the flexibily of the method by using it in conjunction with DualMeshUDF, a state of the art dual meshing method that can operate on UDFs, improving its results and removing the need to tune its parameters.

MeshUDF: Fast and Differentiable Meshing of Unsigned Distance Field Networks

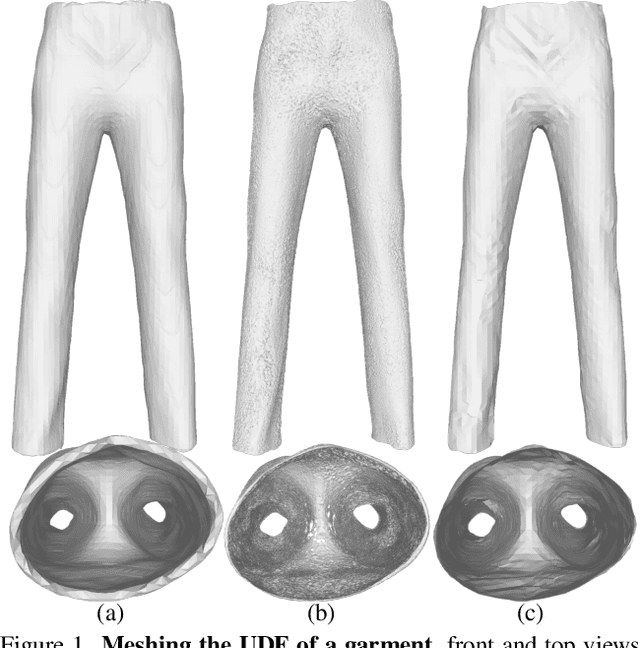
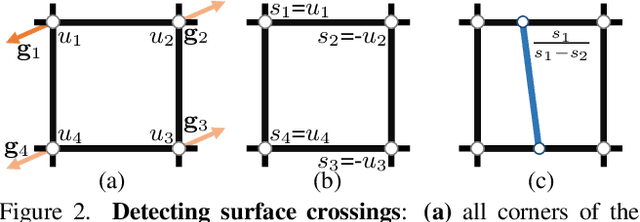
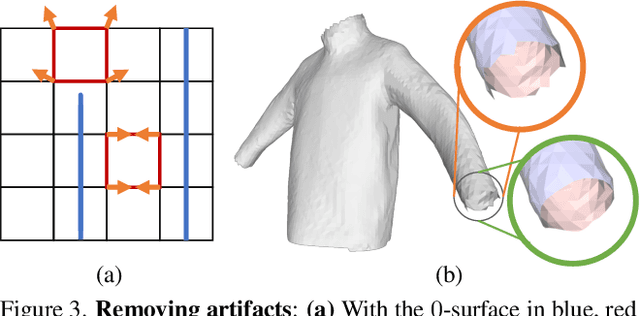
Recent work modelling 3D open surfaces train deep neural networks to approximate Unsigned Distance Fields (UDFs) and implicitly represent shapes. To convert this representation to an explicit mesh, they either use computationally expensive methods to mesh a dense point cloud sampling of the surface, or distort the surface by inflating it into a Signed Distance Field (SDF). By contrast, we propose to directly mesh deep UDFs as open surfaces with an extension of marching cubes, by locally detecting surface crossings. Our method is order of magnitude faster than meshing a dense point cloud, and more accurate than inflating open surfaces. Moreover, we make our surface extraction differentiable, and show it can help fit sparse supervision signals.

Learning to Orient Surfaces by Self-supervised Spherical CNNs

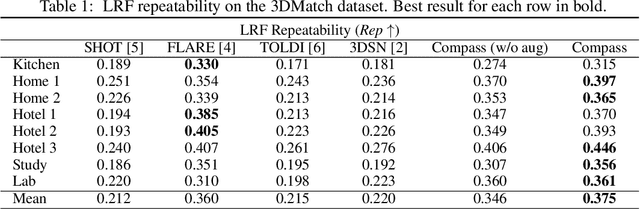
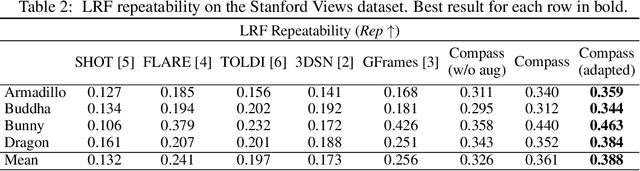
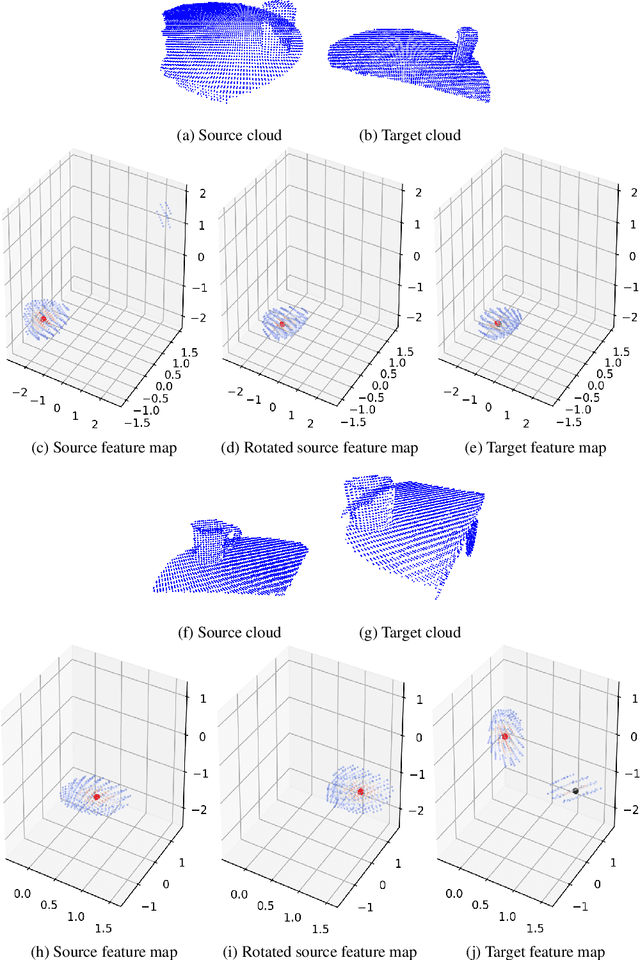
Defining and reliably finding a canonical orientation for 3D surfaces is key to many Computer Vision and Robotics applications. This task is commonly addressed by handcrafted algorithms exploiting geometric cues deemed as distinctive and robust by the designer. Yet, one might conjecture that humans learn the notion of the inherent orientation of 3D objects from experience and that machines may do so alike. In this work, we show the feasibility of learning a robust canonical orientation for surfaces represented as point clouds. Based on the observation that the quintessential property of a canonical orientation is equivariance to 3D rotations, we propose to employ Spherical CNNs, a recently introduced machinery that can learn equivariant representations defined on the Special Orthogonal group SO(3). Specifically, spherical correlations compute feature maps whose elements define 3D rotations. Our method learns such feature maps from raw data by a self-supervised training procedure and robustly selects a rotation to transform the input point cloud into a learned canonical orientation. Thereby, we realize the first end-to-end learning approach to define and extract the canonical orientation of 3D shapes, which we aptly dub Compass. Experiments on several public datasets prove its effectiveness at orienting local surface patches as well as whole objects.