Blankets Joint Posterior score for learning Markov network structures

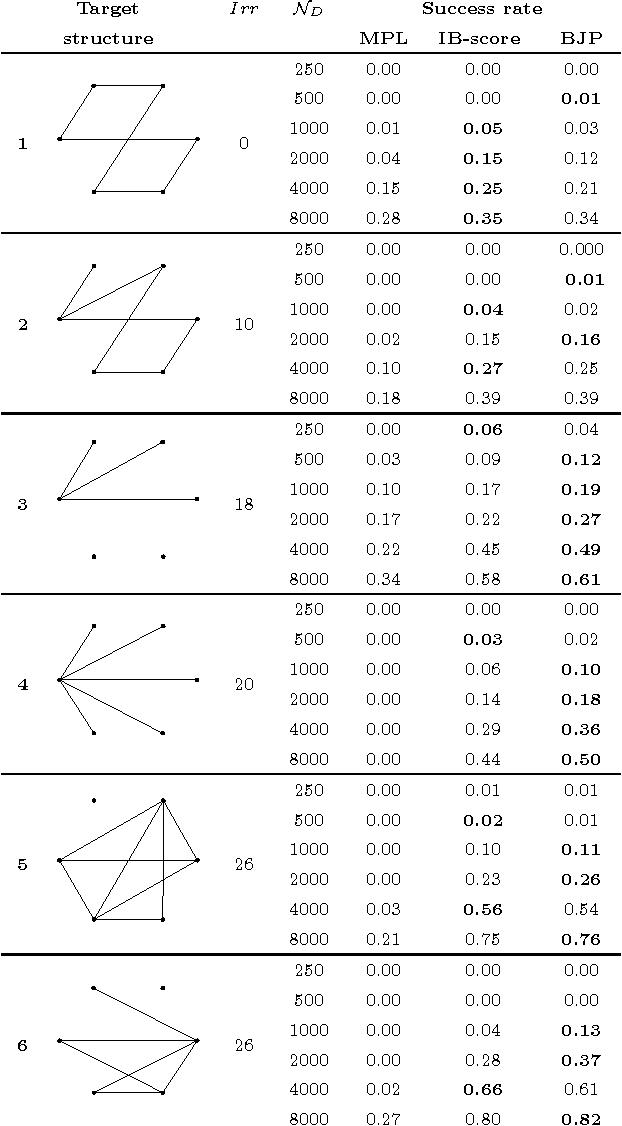
Markov networks are extensively used to model complex sequential, spatial, and relational interactions in a wide range of fields. By learning the structure of independences of a domain, more accurate joint probability distributions can be obtained for inference tasks or, more directly, for interpreting the most significant relations among the variables. Recently, several researchers have investigated techniques for automatically learning the structure from data by obtaining the probabilistic maximum-a-posteriori structure given the available data. However, all the approximations proposed decompose the posterior of the whole structure into local sub-problems, by assuming that the posteriors of the Markov blankets of all the variables are mutually independent. In this work, we propose a scoring function for relaxing such assumption. The Blankets Joint Posterior score computes the joint posterior of structures as a joint distribution of the collection of its Markov blankets. Essentially, the whole posterior is obtained by computing the posterior of the blanket of each variable as a conditional distribution that takes into account information from other blankets in the network. We show in our experimental results that the proposed approximation can improve the sample complexity of state-of-the-art scores when learning complex networks, where the independence assumption between blanket variables is clearly incorrect.

The IBMAP approach for Markov networks structure learning

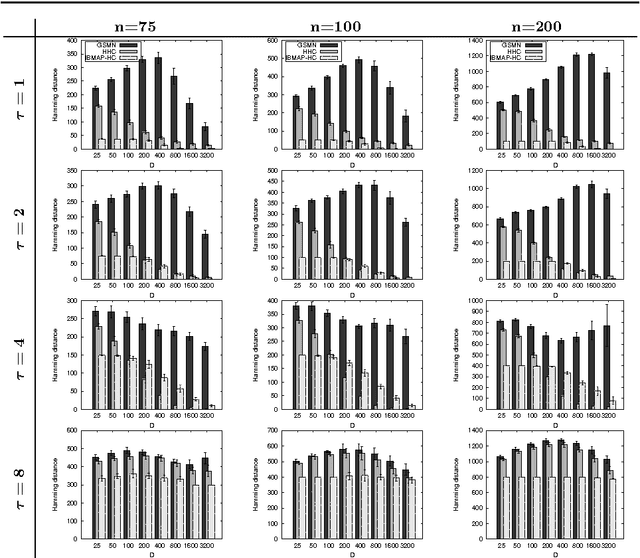
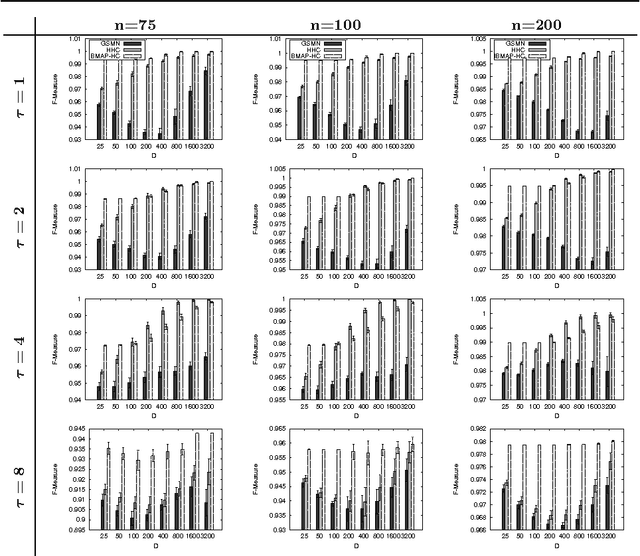
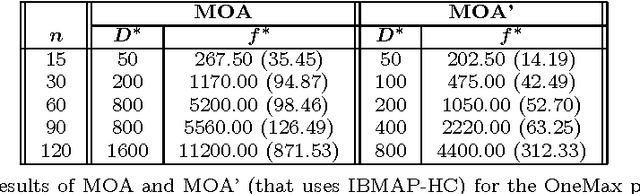
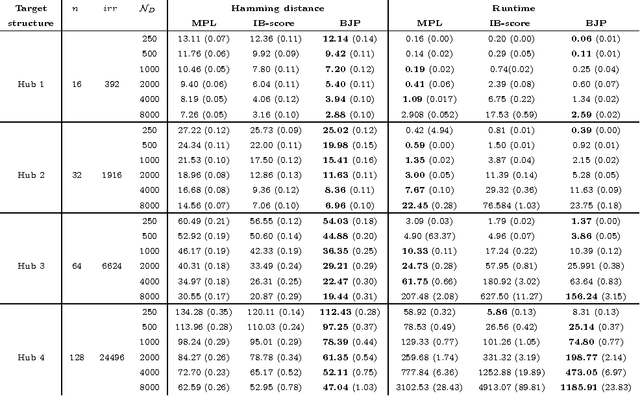
In this work we consider the problem of learning the structure of Markov networks from data. We present an approach for tackling this problem called IBMAP, together with an efficient instantiation of the approach: the IBMAP-HC algorithm, designed for avoiding important limitations of existing independence-based algorithms. These algorithms proceed by performing statistical independence tests on data, trusting completely the outcome of each test. In practice tests may be incorrect, resulting in potential cascading errors and the consequent reduction in the quality of the structures learned. IBMAP contemplates this uncertainty in the outcome of the tests through a probabilistic maximum-a-posteriori approach. The approach is instantiated in the IBMAP-HC algorithm, a structure selection strategy that performs a polynomial heuristic local search in the space of possible structures. We present an extensive empirical evaluation on synthetic and real data, showing that our algorithm outperforms significantly the current independence-based algorithms, in terms of data efficiency and quality of learned structures, with equivalent computational complexities. We also show the performance of IBMAP-HC in a real-world application of knowledge discovery: EDAs, which are evolutionary algorithms that use structure learning on each generation for modeling the distribution of populations. The experiments show that when IBMAP-HC is used to learn the structure, EDAs improve the convergence to the optimum.

A survey on independence-based Markov networks learning

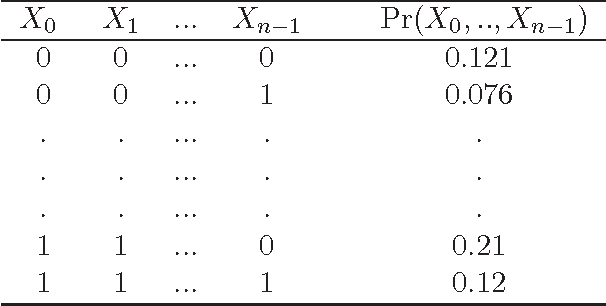
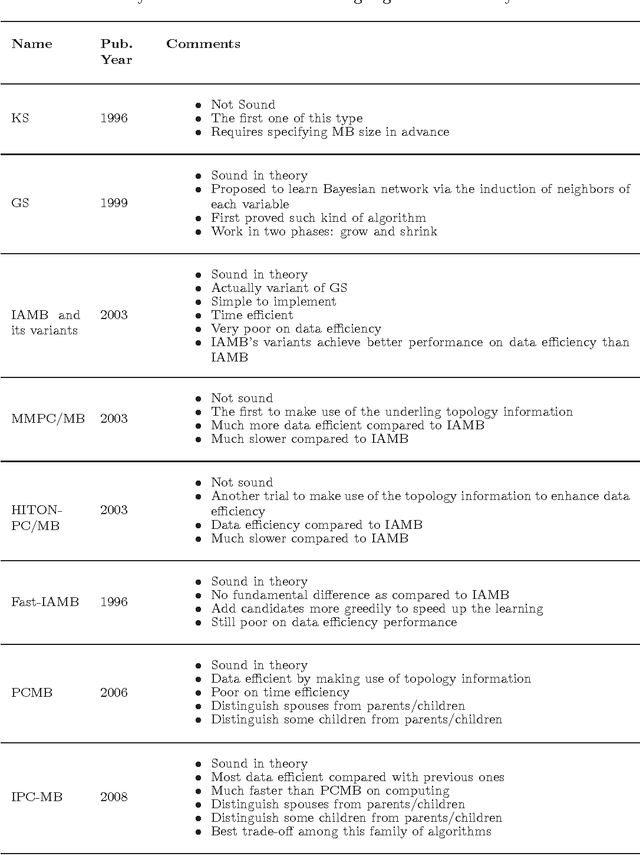
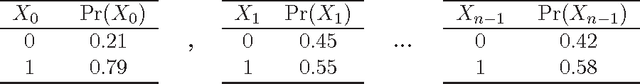
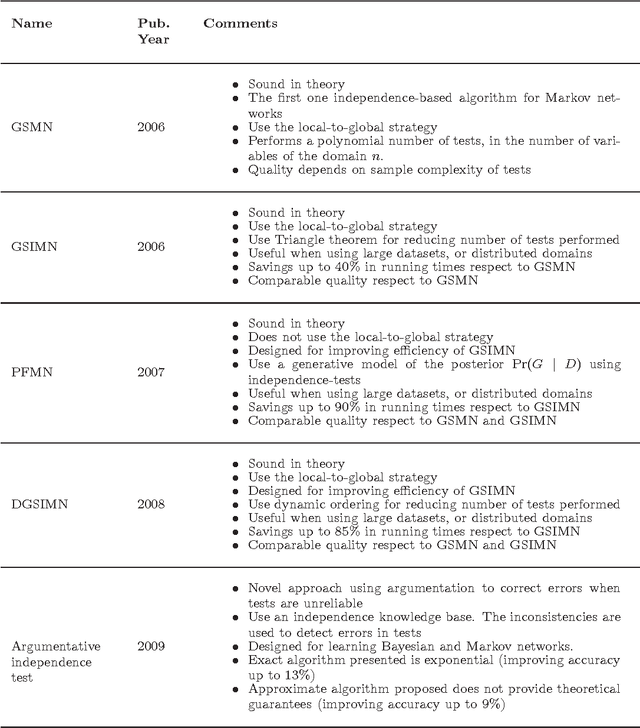
This work reports the most relevant technical aspects in the problem of learning the \emph{Markov network structure} from data. Such problem has become increasingly important in machine learning, and many other application fields of machine learning. Markov networks, together with Bayesian networks, are probabilistic graphical models, a widely used formalism for handling probability distributions in intelligent systems. Learning graphical models from data have been extensively applied for the case of Bayesian networks, but for Markov networks learning it is not tractable in practice. However, this situation is changing with time, given the exponential growth of computers capacity, the plethora of available digital data, and the researching on new learning technologies. This work stresses on a technology called independence-based learning, which allows the learning of the independence structure of those networks from data in an efficient and sound manner, whenever the dataset is sufficiently large, and data is a representative sampling of the target distribution. In the analysis of such technology, this work surveys the current state-of-the-art algorithms for learning Markov networks structure, discussing its current limitations, and proposing a series of open problems where future works may produce some advances in the area in terms of quality and efficiency. The paper concludes by opening a discussion about how to develop a general formalism for improving the quality of the structures learned, when data is scarce.

Learning Markov networks with context-specific independences

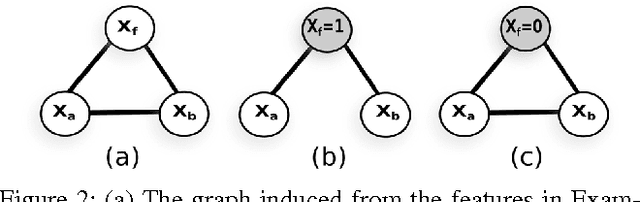
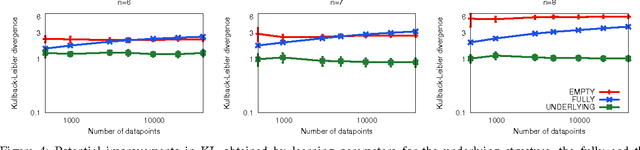
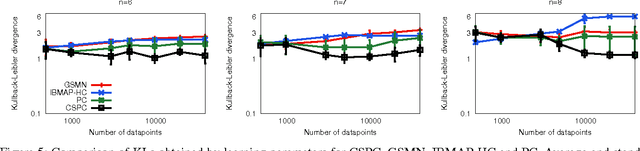
Learning the Markov network structure from data is a problem that has received considerable attention in machine learning, and in many other application fields. This work focuses on a particular approach for this purpose called independence-based learning. Such approach guarantees the learning of the correct structure efficiently, whenever data is sufficient for representing the underlying distribution. However, an important issue of such approach is that the learned structures are encoded in an undirected graph. The problem with graphs is that they cannot encode some types of independence relations, such as the context-specific independences. They are a particular case of conditional independences that is true only for a certain assignment of its conditioning set, in contrast to conditional independences that must hold for all its assignments. In this work we present CSPC, an independence-based algorithm for learning structures that encode context-specific independences, and encoding them in a log-linear model, instead of a graph. The central idea of CSPC is combining the theoretical guarantees provided by the independence-based approach with the benefits of representing complex structures by using features in a log-linear model. We present experiments in a synthetic case, showing that CSPC is more accurate than the state-of-the-art IB algorithms when the underlying distribution contains CSIs.

Markov random fields factorization with context-specific independences

Markov random fields provide a compact representation of joint probability distributions by representing its independence properties in an undirected graph. The well-known Hammersley-Clifford theorem uses these conditional independences to factorize a Gibbs distribution into a set of factors. However, an important issue of using a graph to represent independences is that it cannot encode some types of independence relations, such as the context-specific independences (CSIs). They are a particular case of conditional independences that is true only for a certain assignment of its conditioning set; in contrast to conditional independences that must hold for all its assignments. This work presents a method for factorizing a Markov random field according to CSIs present in a distribution, and formally guarantees that this factorization is correct. This is presented in our main contribution, the context-specific Hammersley-Clifford theorem, a generalization to CSIs of the Hammersley-Clifford theorem that applies for conditional independences.

Efficient Independence-Based MAP Approach for Robust Markov Networks Structure Discovery

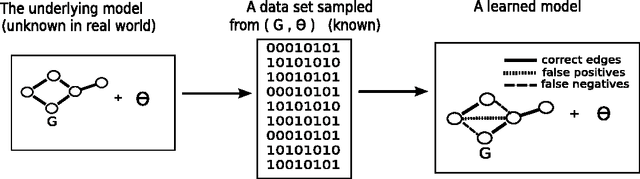
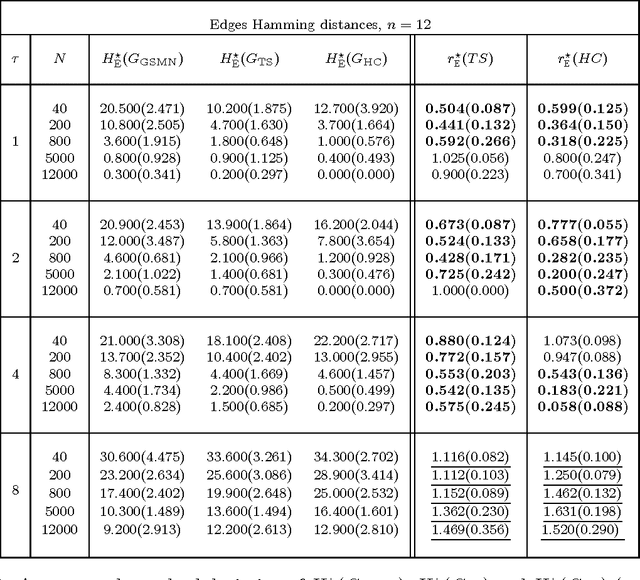
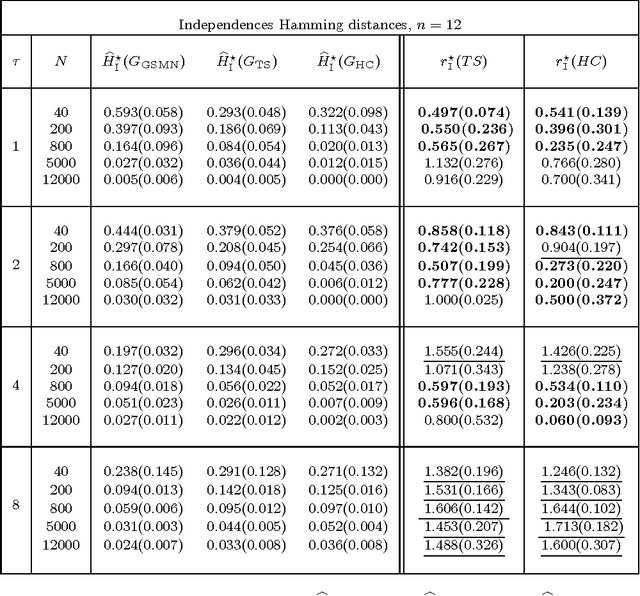
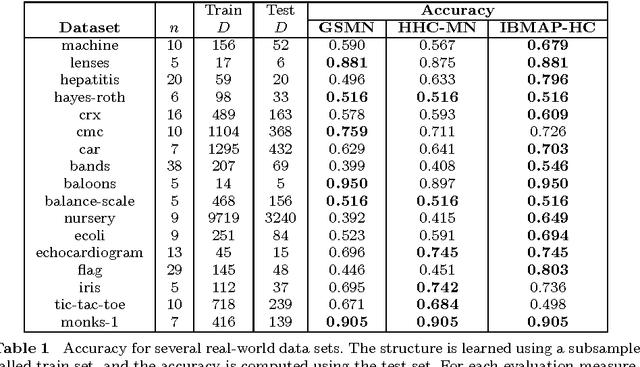
This work introduces the IB-score, a family of independence-based score functions for robust learning of Markov networks independence structures. Markov networks are a widely used graphical representation of probability distributions, with many applications in several fields of science. The main advantage of the IB-score is the possibility of computing it without the need of estimation of the numerical parameters, an NP-hard problem, usually solved through an approximate, data-intensive, iterative optimization. We derive a formal expression for the IB-score from first principles, mainly maximum a posteriori and conditional independence properties, and exemplify several instantiations of it, resulting in two novel algorithms for structure learning: IBMAP-HC and IBMAP-TS. Experimental results over both artificial and real world data show these algorithms achieve important error reductions in the learnt structures when compared with the state-of-the-art independence-based structure learning algorithm GSMN, achieving increments of more than 50% in the amount of independencies they encode correctly, and in some cases, learning correctly over 90% of the edges that GSMN learnt incorrectly. Theoretical analysis shows IBMAP-HC proceeds efficiently, achieving these improvements in a time polynomial to the number of random variables in the domain.